VOLUME 2 - 8. POUTRES TREILLIS

Une poutre à treillis est une structure formée par un agencement triangulaire d'éléments linéaires (ou quasi linéaires) dont les extrémités sont reliées au niveau de points d'assemblage appelés nœuds. Les poutres à treillis se composent de triangles, c’est-à-dire des formes géométriquement stables. En effet, un triangle présente des angles fixes qui ne peuvent être ni agrandis, ni rétrécis sans céder au niveau des points d'assemblage, contrairement, notamment, à un rectangle, lequel peut devenir un parallélogramme.

Dans une poutre à treillis plan, l'ensemble des éléments et des nœuds sont situés dans un plan en deux dimensions, tandis que dans une poutre à treillis spatial, les éléments et les nœuds se développent dans les trois dimensions. Les poutres à treillis en bois consistent généralement en un agencement plan en appui simple sur deux points. La suite de ce chapitre est consacrée à ce type de poutre.

Les poutres à treillis en bois offrent une solution économique en présence de portées supérieures à 25-30 m. L'un des avantages de la conception à treillis pour les toitures est la possibilité d'installer les conduits et les tuyaux nécessaires au fonctionnement des installations techniques du bâtiment à travers l'âme en treillis.

Dans les cas de portées importantes où des spécifications de toitures plus légères sont probables, les poutres à treillis sont espacées de 5 à 12 m de centre à centre, supportent des pannes espacées d'1,2 à 2,4 m et soutiennent un bac acier. En guise d’alternative aux pannes, un bac acier plus lourd est appliqué directement sur les poutres. Il est généralement possible de réaliser des économies en augmentant l'espacement des poutres parallèlement à leur portée.

8.1. GEOMETRIE DES POUTRES A TREILLIS

La fonction structurelle d'une poutre à treillis est de supporter et de transférer les charges depuis les points d'application (généralement les pannes) vers les points d'appui d’une manière aussi efficace et économique que possible. Cette efficacité repose sur le choix d'un type de poutre à treillis adapté aux exigences architecturales et aux conditions de charge. Des modèles types « idéalisés » de poutres à treillis utilisées dans deux types de conditions de charge sont représentés à la Figure 8.1.

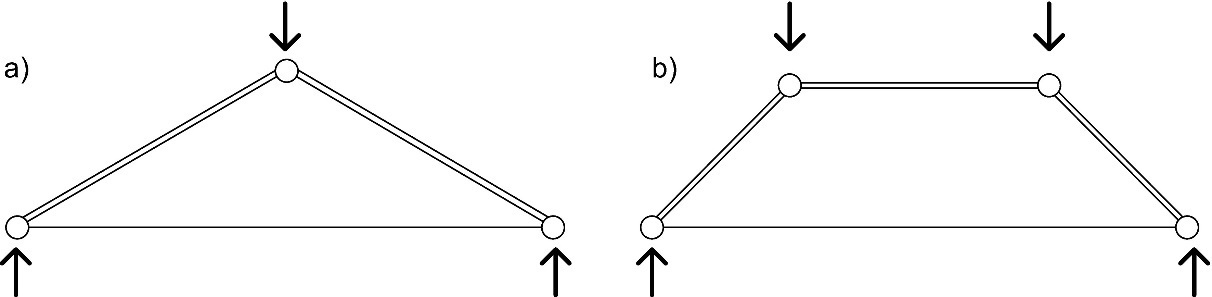
Figure 8.1 : Exemples d’agencements idéalisés de poutres à treillis dans deux conditions de charge : (a) structure en treillis à trois articulations stable ; (b) mécanisme à quatre articulations instable.

Dans un système à charge symétrique (d'une importance particulière dans le cas illustré à la Figure 8.1(b), à savoir une structure à quatre articulations et donc instable), le transfert de charge est opéré sans barres de treillis internes, dans la mesure où le funiculaire des forces concorde avec la géométrie de la structure. Malheureusement, il est rarement possible de pouvoir utiliser une configuration sans ces éléments internes, étant donné qu’un déséquilibre de charge peut se produire quasi systématiquement du fait de la neige, du vent ou de charges permanentes. Ce déséquilibre peut également être lié à des tolérances de montage et de fabrication. Néanmoins, l'ingénieur devra essayer d'utiliser un profil à treillis proche de celui idéalisé (funiculaire des charges), en intégrant un système triangulé capable de prendre en charge un tel déséquilibre. Ainsi, les forces intervenant au niveau des éléments internes et de leurs assemblages seront limitées au minimum, avec l’avantage d’une conception à la fois simple et économique. Deux systèmes triangulés envisageables pour le cas de la Figure 8.1(b) sont présentés à la Figure 8.2.

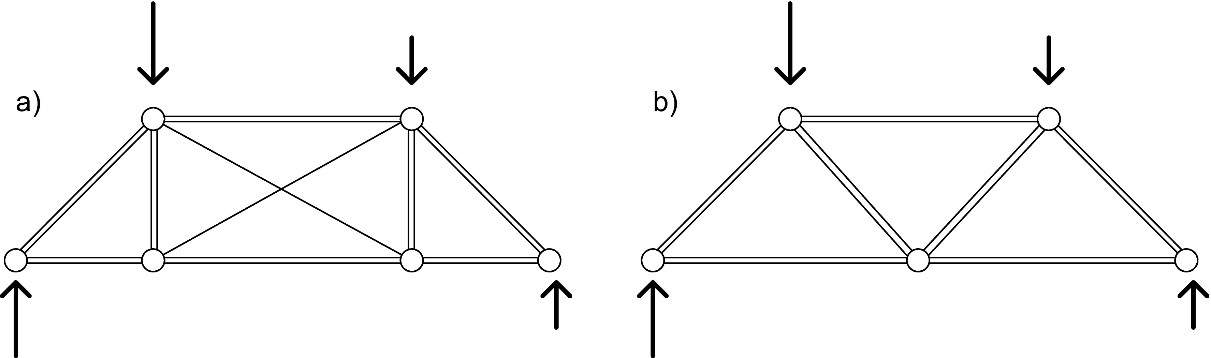
Figure 8.2 : Exemples de systèmes triangulés supportant les déséquilibres de charge.

Si le profil architectural requis s'oppose au profil structurel « optimal », des contraintes importantes peuvent être générées dans le système triangulé et les assemblages. La maîtrise des coûts de la structure passera alors par l’adoption de l'agencement structurel interne le mieux adapté, lequel constituera un compromis économique entre les matériaux et la main-d'œuvre. Pour ce faire, plusieurs aspects devront être pris en compte, à savoir :

Le nombre d'assemblages devra être le plus faible possible, compte tenu du coût élevé de réalisation de chacun d’entre eux, et dans la mesure où le glissement de ces assemblages à chaque nœud amplifiera la flèche de la poutre à treillis ;
L'élancement des membrures comprimées et des contrefiches internes ne devra pas être excessif ; › La flexion locale des membrures ne devra pas être trop grande ; et
L'angle entre les membrures et les diagonales internes ne devra pas être trop faible.

Le transport constitue fréquemment une contrainte dans le cas de poutres à treillis présentant une hauteur et une portée importantes. Les poutres mesurant plus de 3 m de haut ou plus de 20-25 m de long requièrent une attention particulière. Ce problème de transport peut généralement être pallié en procédant au démontage partiel ou intégral de la poutre.

Les principaux éléments des grandes poutres à treillis peuvent être joints en un ou plusieurs endroits de la travée. Parfois, l'assemblage peut être intégralement réalisé sur place. Cependant, il est toujours préférable de procéder à un assemblage initial à l'usine, afin de garantir un assemblage et un démontage adéquats pour le transport. Les grandes fermes (cf. exemple de la Figure 8.4 (c)) peuvent être fabriquées en deux parties puis assemblées sur site à l'aide d'un joint de continuité.

Il existe un large éventail de formes générales possibles pour les poutres à treillis, l'une des plus courantes pour les poutres lamellées-collées étant la ferme à trois articulations. Cette forme est abordée au Chapitre 9. D'autres formes très utilisées sont décrites aux sections suivantes.

8.1.1. Poutres à membrures parallèles

En règle générale, les poutres à membrures parallèles sont indiquées comme alternatives aux poutres lamellées-collées ou à âme de longues portées (25-30 m), et ce, pour des raisons économiques. Les charges appliquées aux barres de treillis sont souvent très importantes, d'où des difficultés à réaliser des points d'assemblage adéquats. Les systèmes triangulés généralement choisis sont les suivants : le type Howe (diagonales comprimées, Figure 8.3 (a)), le type Pratt (diagonales tendues, Figure 8.3 (b)), et le type Warren (diagonales comprimées et tendues, Figure 8.3 (c)).

Figure 8.3 : Exemples de poutres à membrures parallèles : (a) type Howe (diagonales comprimées), (b) type Pratt (diagonales tendues), (c) type Warren (diagonales comprimées et tendues).

L'avantage d'utiliser un système aux diagonales comprimées plutôt qu’aux diagonales tendues tient au fait que les points d'assemblage entre les diagonales et les membrures sont de construction simple, dans la mesure où ils peuvent transmettre les charges par réaction d’appui. Son inconvénient : les diagonales relativement longues seront comprimées, et donc sujettes au flambement. Le système de type Pratt offre l’avantage de pouvoir être également soutenu au niveau de sa membrure supérieure, comme illustré à la Figure 8.3 (b). Par conséquent, le centre de gravité de la poutre se trouve en dessous de l’axe reliant les deux appuis. Cette solution facilite les opérations de montage, compte tenu du fait qu'en cas de dévers initial, le poids propre de la poutre agit comme force stabilisatrice empêchant tout renversement.

Les poutres à membrures parallèles sont généralement conçues avec une contre-flèche, laquelle correspond approximativement à la flèche induite par le poids propre de la structure éventuellement majoré de la moitié de la charge variable principale (par ex. charge de neige).

8.1.2. Fermes

En cas de charges uniformément réparties, la forme des fermes est relativement adaptée au diagramme des moments de flexion et permet l'utilisation de matériaux de couvertures classiques tels que les pannes et/ou les bacs acier. Une partie de la charge appliquée est transférée directement à travers la membrure supérieure vers les points d'appui, tandis que les barres de treillis transfèrent les charges d'une amplitude relativement petite à moyenne. Les points d'assemblage sont, quant à eux, conçus pour absorber ces charges en toute facilité. En ce qui concerne les fermes à membrure inférieure horizontale, des systèmes triangulés similaires à ceux présentés à la Figure 8.3 peuvent être utilisés. La Figure 8.4 montre différents types de fermes à double pente.

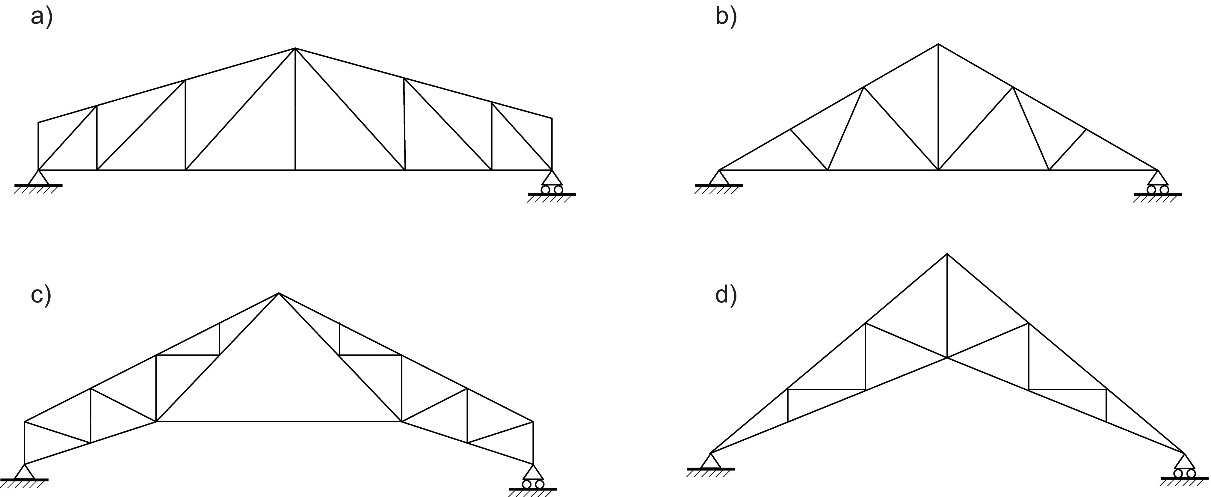
Figure 8.4 : Exemples de fermes à double pente : (a) trapézoïdale (type Howe), (b) triangulaire à membrure inférieure horizontale, (c) triangulaire à entrait retroussé, (d) ferme à écharpes.

Les fermes à double pente peuvent présenter un entrait retroussé de manière à offrir un espace supplémentaire au centre (cf. Figure 8.4, (c) et (d)). Ces structures peuvent s'avérer particulièrement utiles pour les bâtiments de stockage disposant d'un accès central.

8.1.3. Poutres bow string et lenticulaires

Pour les applications de grandes portées, les poutres à treillis bow-string et lenticulaires (Figure 8.5) peuvent constituer une solution très économique. Grâce à une sollicitation uniforme et à une faible concentration de charge, les membrures de la poutre à treillis supportent quasiment toutes les charges appliquées. Ainsi, les barres de treillis sont très faiblement sollicitées, d’où une conception simple et peu coûteuse des assemblages entre les diagonales et les membrures. Ces systèmes statiques permettent d'obtenir en toute facilité des poutres à treillis lamellées-collées d'une portée supérieure à 60-70 m.

D'un point de vue de la statique, un profil parabolique est la solution la plus efficace pour supporter une charge uniforme. Cependant, dans la pratique, il s'avère plus adapté (ou nécessaire) d'adopter un profil circulaire pour les membrures. La membrure supérieure des poutres bow-string et chacune des membrures des poutres lenticulaires consistent généralement en au moins deux éléments lamellés-collés courbes à assemblage rigide. La membrure inférieure des poutres bow-string comprend plusieurs tiges métalliques.

Figure 8.5 : Exemples de poutres bow-string et lenticulaire : (a) poutre bow-string à membrure inférieure horizontale, (b) poutre bow-string à entrait retroussé, (c) poutre lenticulaire.

8.1.4. Efforts dans les barres de treillis

Comme mentionné précédemment, le choix du type de structure influe grandement sur l'amplitude des efforts normaux agissant dans les barres de treillis. Afin d'illustrer la différence d'amplitude des forces appliquées aux éléments en fonction du type de poutre, des coefficients de forces sont présentés à la Figure 8.6 pour trois modèles types de poutres à treillis selon des rapports portée-hauteur typiques. Ces coefficients montrent l'amplitude des forces dans les barres ; ils sont définis comme le rapport N/(q*l), où N désigne la force agissant dans la barre, q désigne une charge unitaire uniformément répartie et l désigne la portée de la poutre. La partie gauche de la figure concerne des poutres en appui simple soumises à une charge unitaire uniformément répartie (q=1) ; la partie droite concerne des poutres similaires, mais soumises à une charge déséquilibrée (q_l = 1 sur la moitié gauche et q_r = 0,5 sur la moitié droite). Les chiffres en rouge indiquent les valeurs en traction ; les chiffres en bleu indiquent les valeurs en compression.

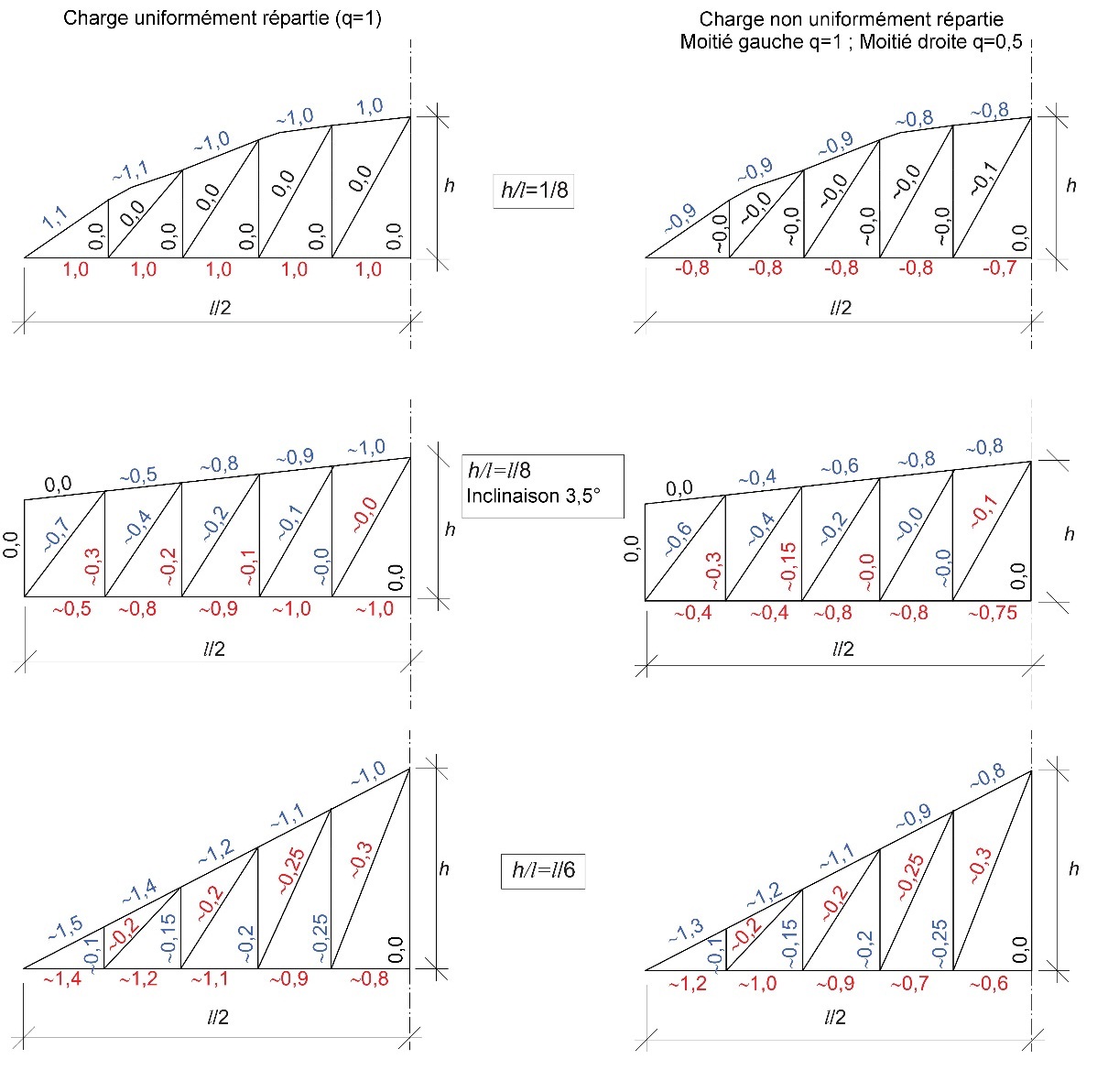
Figure 8.6 : Amplitude des efforts normaux dans trois différents types de poutres à treillis : bow-string (en haut), ferme
trapézoïdale (au milieu) et ferme triangulée (en bas). À gauche : charge unitaire uniformément répartie (q=1) ; à droite :
charge déséquilibrée (q_l=1 sur la moitié gauche et q_r=0,5 sur la moitié droite).

Comme illustré à la Figure 8.6, dans les poutres bow-string à membrure supérieure parabolique, la traction et la compression sont quasiment constantes dans chaque membrure. Par conséquent, les barres de treillis (montants et diagonales) ne seront quasiment pas sollicitées. D'où des assemblages - hormis ceux entre les membrures supérieure et inférieure au niveau de l'appui et les éventuels joints de montage dans la membrure inférieure - relativement peu coûteux pour ce type de poutres.

Des efforts normaux importants interviennent dans les diagonales des fermes trapézoïdales, particulièrement dans celles les plus proches des appuis. C'est pourquoi la réalisation d'assemblages peut s'avérer compliquée en ces endroits. De plus, une attention spécifique devra être portée au flambement de ces diagonales.

Dans les fermes triangulées, des efforts normaux relativement faibles se produisent dans les barres de treillis. Cependant, dans les membrures supérieure et inférieure, respectivement, des forces de compression et de traction très importantes agissent à proximité des appuis.

Il convient toutefois de noter que certaines répartitions de charges induites par l'accumulation de neige (par ex. répartitions triangulaires de charge sur chaque moitié de la poutre) peuvent générer des forces dans les barres de treillis, lesquelles peuvent différer significativement de celles présentées à la Figure 8.6.

8.2. ETUDE DE CONCEPTION

En règle générale, les aspects architecturaux déterminent la forme et, le cas échéant, la pente de la toiture. La nécessité de faire passer des installations (conduits d'aération, par exemple) au travers de la poutre à treillis peut également influer sur le choix du profil. Cependant, pour des raisons économiques, il conviendra de suivre les règles générales concernant les rapports hauteur-portée, la portée maximale, etc. La Figure 8.7 propose des indications de calcul préliminaire pour trois modèles types de poutres à treillis.

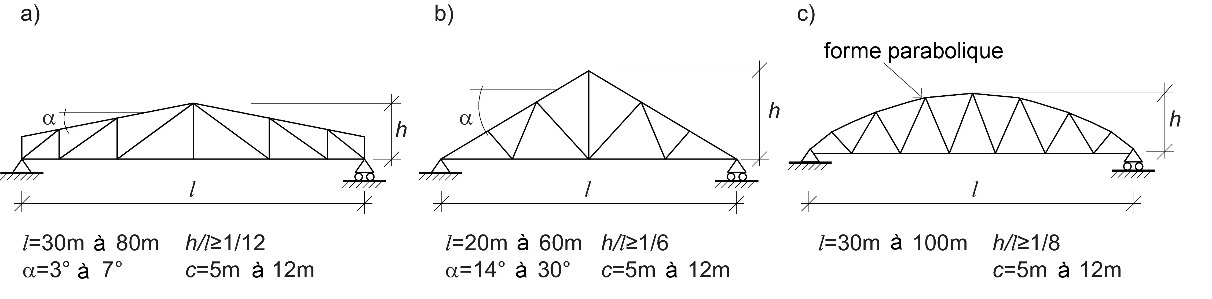
Figure 8.7 : Calcul préliminaire de trois différents types de poutres à treillis. « c » correspond à la distance centre à centre entre les poutres adjacentes.

Les aspects détaillés ci-après devront être pris en compte dans le cadre du calcul préliminaire :

Le système porteur secondaire (par ex. pannes perpendiculaires aux poutres), devra être adapté au système triangulé de la poutre, de sorte que les charges soient transmises au niveau des nœuds (ou le plus proche possible de ces derniers) ;
Par mesure d'économie, le modèle avec les diagonales comprimées (par ex. type Howe) est généralement préféré pour les poutres à treillis en bois dont les éléments doivent être soumis à des charges modérées. Si les diagonales sont tendues, les nœuds devront transmettre les forces de traction. Dans les structures en bois, les nœuds soumis à traction sont en principe plus compliqués et plus longs à construire, et ils impliquent presque systématiquement des assemblages métalliques pour transférer les forces d'un élément à un autre. En revanche, une poutre à treillis conçue avec des diagonales comprimées permet à ces dernières de transférer leurs forces vers les éléments horizontaux et verticaux par appui direct sur ces derniers ; de plus, les éléments en bois sont suffisamment épais pour réduire tout risque de flambement comparé, par exemple, à des éléments métalliques. Lorsque les charges agissant dans une barre de treillis sont très importantes, cependant, la transmission de charges par réaction aux appuis peut ne pas suffire. Dans ce cas, l'utilisation d'assemblages métalliques serait indispensable ; l'agencement des diagonales (tendues ou comprimées) n'aurait alors aucune incidence sur le coût ;
Afin de garantir une bonne efficacité de la poutre à treillis, l'angle entre les diagonales et les membrures devra être proche de 45° ±15^o .

8.2.1. Dimensionnement préliminaire des éléments

L’aire transversale des éléments peut être définie de façon préliminaire à partir d'une analyse simplifiée s'appuyant sur un modèle simple avec des articulations à l'extrémité de chaque élément et sans excentricité. Il est ainsi possible d'évaluer rapidement les forces agissant dans les éléments, forces qui serviront de base au calcul préliminaire. Le système statique utilisé pour l'analyse simplifiée de deux profils typiques de poutres à treillis est présenté à la Figure 8.8. À noter que l'approche proposée ci-dessous pour calculer les forces internes est de nature prudente, étant donné qu'elle repose sur l'hypothèse de barres parfaitement articulées.

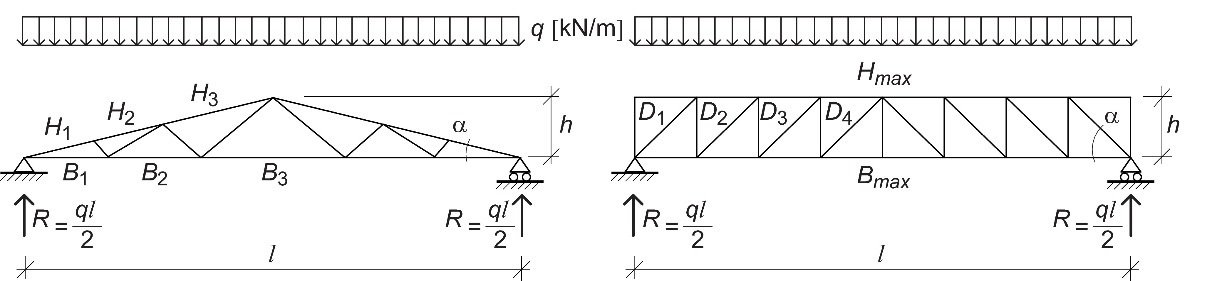
Figure 8.8 : Système statique utilisé pour le calcul préliminaire : (a) ferme à treillis triangulaire et (b) poutre à treillis de type Howe.

8.2.1.1. Ferme à treillis triangulaire

Les forces maximales interviennent au niveau des éléments les plus proches de l'appui. En supposant un modèle d’équilibre au nœud d'appui, la force de traction maximale peut être calculée comme suit :

Pour les profils courants de fermes à treillis triangulaires, la force agissant dans la barre de treillis la plus sollicitée présente une amplitude de l'ordre de 1/5 à 1/3 de H_max.

8.2.1.2. Poutre à treillis triangulaire de type Howe

Les forces maximales présentes dans les membrures se produisent dans la zone à mitravée. La force de traction maximale B_max et la force de compression maximale H_max peuvent être calculées comme suit :

La force maximale présente dans les barres de treillis intervient au niveau de la diagonale la plus proche de l'appui. Selon un modèle d’équilibre, on obtient :

8.2.2. Règles générales concernant le dimensionnement des éléments

Il conviendra de choisir le rapport largeur-hauteur des éléments en fonction du type d'assemblage utilisé pour les nœuds de la poutre à treillis. Par exemple, il peut être envisagé un assemblage fait de broches et de plaques insérées, lequel est couramment utilisé pour les poutres de grande portée (cf. Figure 8.9). Afin d'accroître la capacité résistante des nœuds, il est généralement nécessaire d'utiliser un grand nombre de plaques insérées ; cela implique l'adoption de sections transversales relativement larges pouvant accueillir ces plaques.

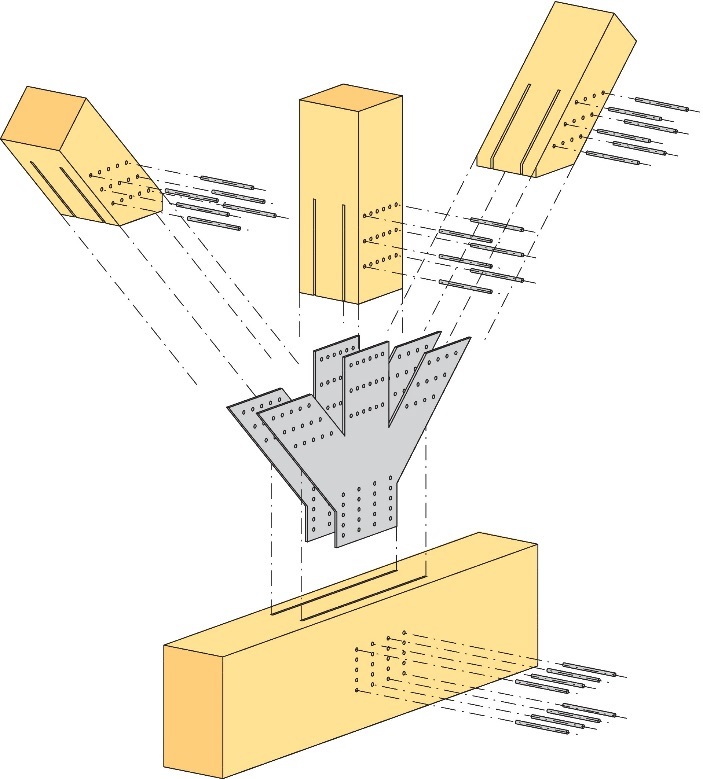
Figure 8.9 : Nœud typique de poutre à treillis incluant des broches et des plaques insérées.

La rigidité à la flexion de chaque élément situé dans le plan de la poutre à treillis devra être maintenue à une valeur raisonnablement faible par rapport à celle de la poutre assemblée. De cette manière, les moments de flexion au niveau des nœuds seront faibles et, en principe, sans importance ; il sera alors possible d'analyser la poutre à treillis selon une approximation satisfaisante, en supposant que tous ces membres sont articulés à leurs extrémités. L'hypothèse selon laquelle la rigidité à la flexion des éléments est faible comparée à celle de la poutre assemblée se vérifie en général, à condition que les hauteurs des membrures ne dépassent pas 1/7 de la hauteur de la poutre (cf. Figure 8.10).

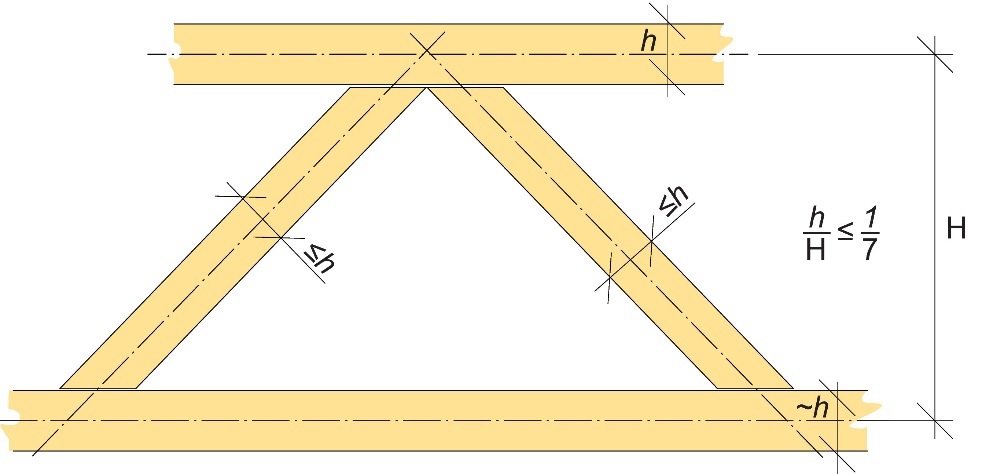
Figure 8.10 : Rapport entre les hauteurs des éléments et la hauteur de la poutre de manière à réduire l'impact de moments de flexion.

C'est pourquoi des sections transversales presque carrées sont généralement utilisées pour les éléments comprimés, tandis que des sections carrées ou rectangulaires (le côté le plus long étant placé dans le sens perpendiculaire au plan de la poutre) sont utilisées pour les éléments tendus. Le choix de sections relativement peu profondes (dans le plan de la poutre) offre également l'avantage de faciliter la conception de nœuds sans excentricité.

Toute excentricité devra être évitée au niveau des nœuds, notamment compte tenu du risque de rupture fragile causée par des contraintes de traction perpendiculaires au fil, du fait de moments de flexion secondaires (cf. Figure 8.11). Ainsi, les axes des éléments qui convergent vers un nœud devront se rejoindre en un seul et même point, à savoir l'axe du nœud. Une étude conceptuelle bien pensée permet, dans la plupart des cas, de créer des nœuds sans excentricité.

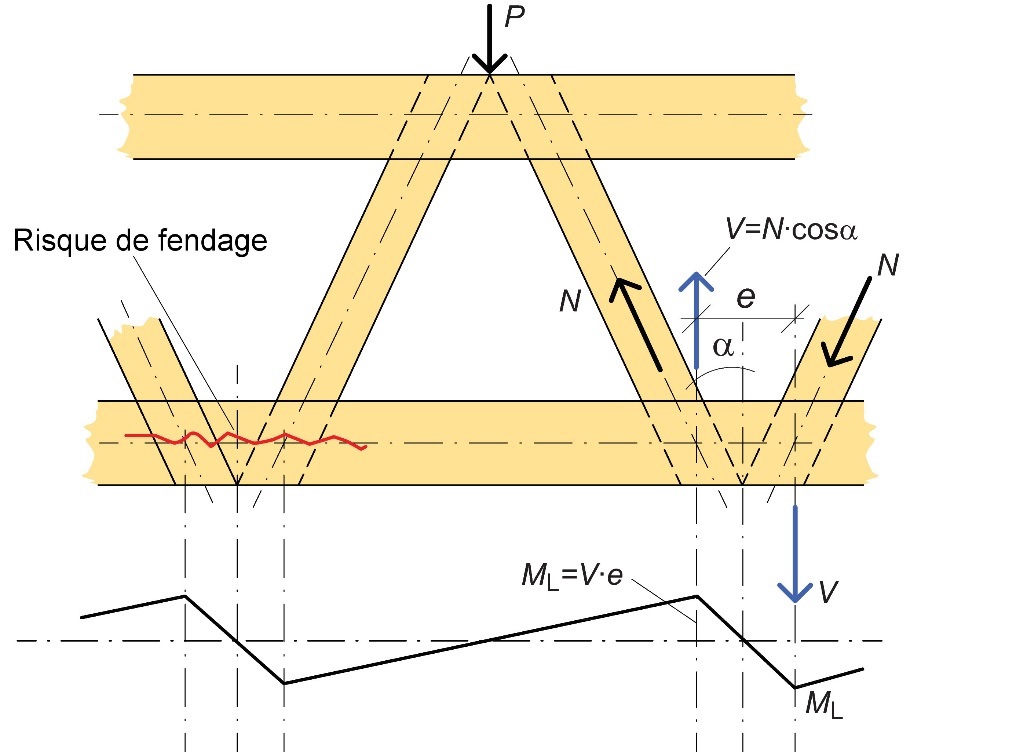
Figure 8.11 : Mauvais exemple de poutre présentant des excentricités au niveau des nœuds. La figure montre également le diagramme des moments d'excentricité et l'emplacement d'une fissure potentiellement provoquée par une traction perpendiculaire au fil.

Dans le cadre du calcul, il est très important d'envisager la réduction de la résistance du fait de la présence de fentes et de trous d'assemblage, particulièrement pour les éléments soumis à une traction. Généralement, au cours du calcul préliminaire, la surface nette A_net peut être considérée comme égale à 60-80 % de la surface brute A_gross des éléments tendus, afin de prendre en compte les fentes et les trous (A_net = 0,7 · A_gross).

Les dimensions de la section transversale des éléments de la poutre à treillis et les types d'assemblages pour les nœuds sont souvent choisis en fonction de la résistance au feu requise pour la structure donnée (classe R60 ou R90).

8.3. CALCUL DES EFFORTS DANS LES ELEMENTS ET LES ASSEMBLAGES

Une poutre à treillis « idéale » serait représentée par un système statique parfaitement articulé à chaque nœud, sans excentricité aux nœuds et avec des charges concentrées exclusivement appliquées aux nœuds (cf. Figure 8.12).

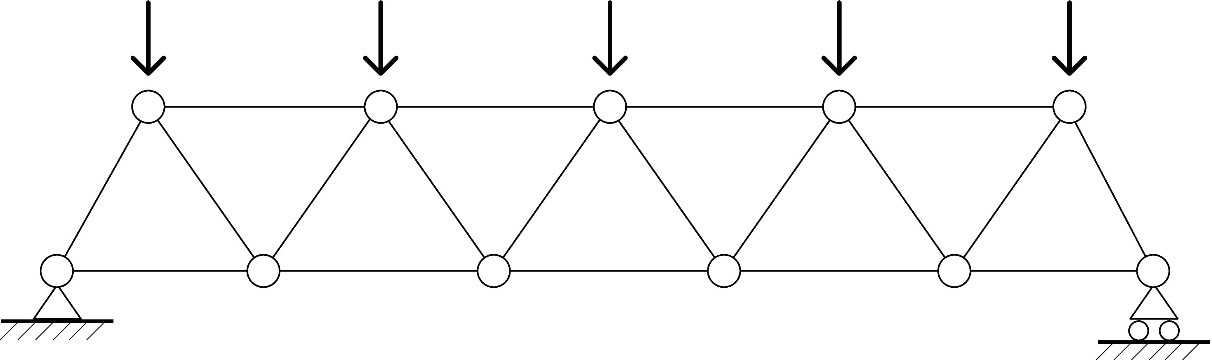
Figure 8.12 : Schématisation d'une poutre à treillis « idéale », aux nœuds articulés et aux charges exclusivement appliquées aux nœuds.

Dans les structures en bois, cependant, une telle situation idéale ne se produit que très rarement. En effet, au niveau des nœuds, les points d'assemblage génèrent un certain degré de maintien en rotation, tandis qu'un glissement intervient du fait de la déformabilité des assemblages. De plus, les membrures supérieure et inférieure de la poutre consistent généralement en des éléments continus non articulés au niveau de leurs intersections avec les barres de treillis, comme c’est le cas de la structure idéale. Un modèle plus avancé inclurait des ressorts de translation et de rotation au niveau des nœuds (cf. Figure 8.13).

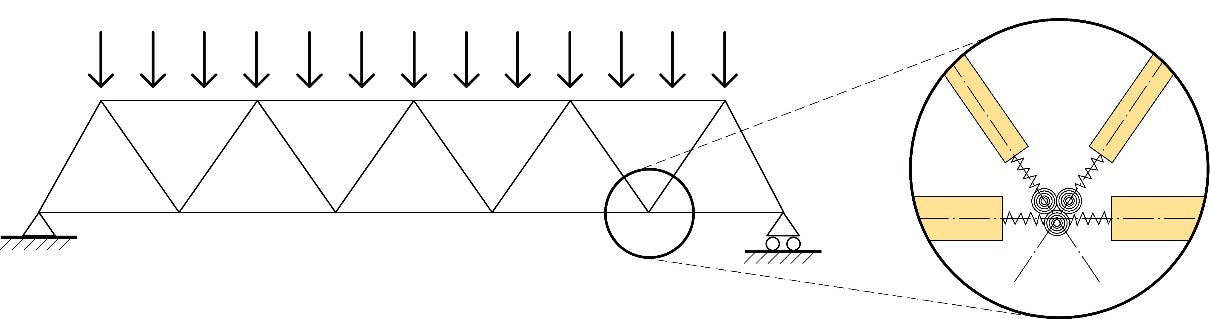
Figure 8.13: Modèle avancé de poutre à treillis comprenant des ressorts de translation et de rotation aux extrémités des barres de treillis.

Cependant, dans la pratique, il est quasiment impossible de déterminer de façon rigoureuse la raideur en rotation et en translation des assemblages. C'est pourquoi il est recommandé d'analyser une condition limite supérieure et une condition limite inférieure, à savoir : i) un système statique comprenant des articulations à l'extrémité de chaque barre de treillis (Figure 8.14 (a)), et ii) un système statique comprenant des barres de treillis fixées aux membrures (Figure 8.14 (b)).

Figure 8.14 : Système statique à analyser pour déterminer les conditions limites des forces et des moments dans les éléments. Les deux poutres possèdent des membrures supérieure et inférieure continues. (a) Poutre aux barres de treillis articulées ; (b) poutre aux barres de treillis rigides sous charge.

Le calcul des éléments peut s'appuyer sur la condition de contrainte la plus intense parmi les exemples (a) et (b) de la Figure 8.14.

Les éléments peuvent être de type simple ou mixte. Les doubles membrures supérieure et inférieure sont généralement associées à des diagonales simples. Les éléments lamellés-collés comprimés sont parfois associés à des éléments tendus en acier (cf. Figure 8.19).

Les éléments tendus doivent être conçus en tenant compte de la réduction des sections transversales en raison de la présence de trous de boulonnage, etc. L'espace requis par les assembleurs, etc., aux nœuds joue un rôle essentiel dans le dimensionnement de ces éléments.

En principe, les assemblages aux nœuds sont conçus comme s'ils étaient soumis à des forces axiales pures. Cependant, les forces axiales calculées devront être majorées d'environ 10 à 15 %, afin de prendre en compte d'éventuelles excentricités (non prévues) et une possible rigidité rotationnelle induite par l'assemblage.

8.3.1. Flambement des éléments comprimés

Les éléments comprimés et les éléments sont soumis à la fois à une compression et à une flexion (généralement situés dans la membrure supérieure de la poutre à treillis) doivent être conçus conformément aux indications du Chapitre 4, en tenant compte du risque de flambement dans le plan de la poutre et hors-plan.

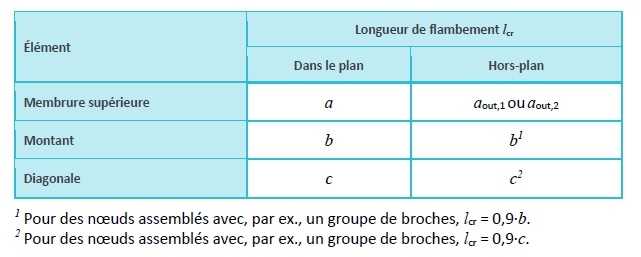
En ce qui concerne les membrures en général, et le flambement hors-plan des barres de treillis, la longueur de flambement lcr peut être prise égale à la longueur du système l. La longueur du système dans le plan correspond à la distance entre les points d'assemblage. La longueur du système hors-plan correspond à la distance entre les appuis latéraux. Les barres de treillis peuvent être calculées pour les cas de flambement dans le plan à partir d'une longueur de flambement inférieure à la longueur du système, à condition que les membrures assurent un encastrement approprié et que les assemblages d'extrémité assurent une rigidité adéquate. Concernant les nœuds assemblés avec, par exemple, des assembleurs consistant en un groupe de broches (cf. Figures 8.16(b) et 8.17), la longueur de flambement lcr des barres de treillis pour le flambement dans le plan peut être prise égale à 0,9·l.

Cependant, en cas de rotations potentielles au niveau des liaisons (par ex. assemblages consistant en un seul boulon), il sera possible d'appliquer une valeur de 1,0 (cf. Figure 8.15 et Tableau 8.1).

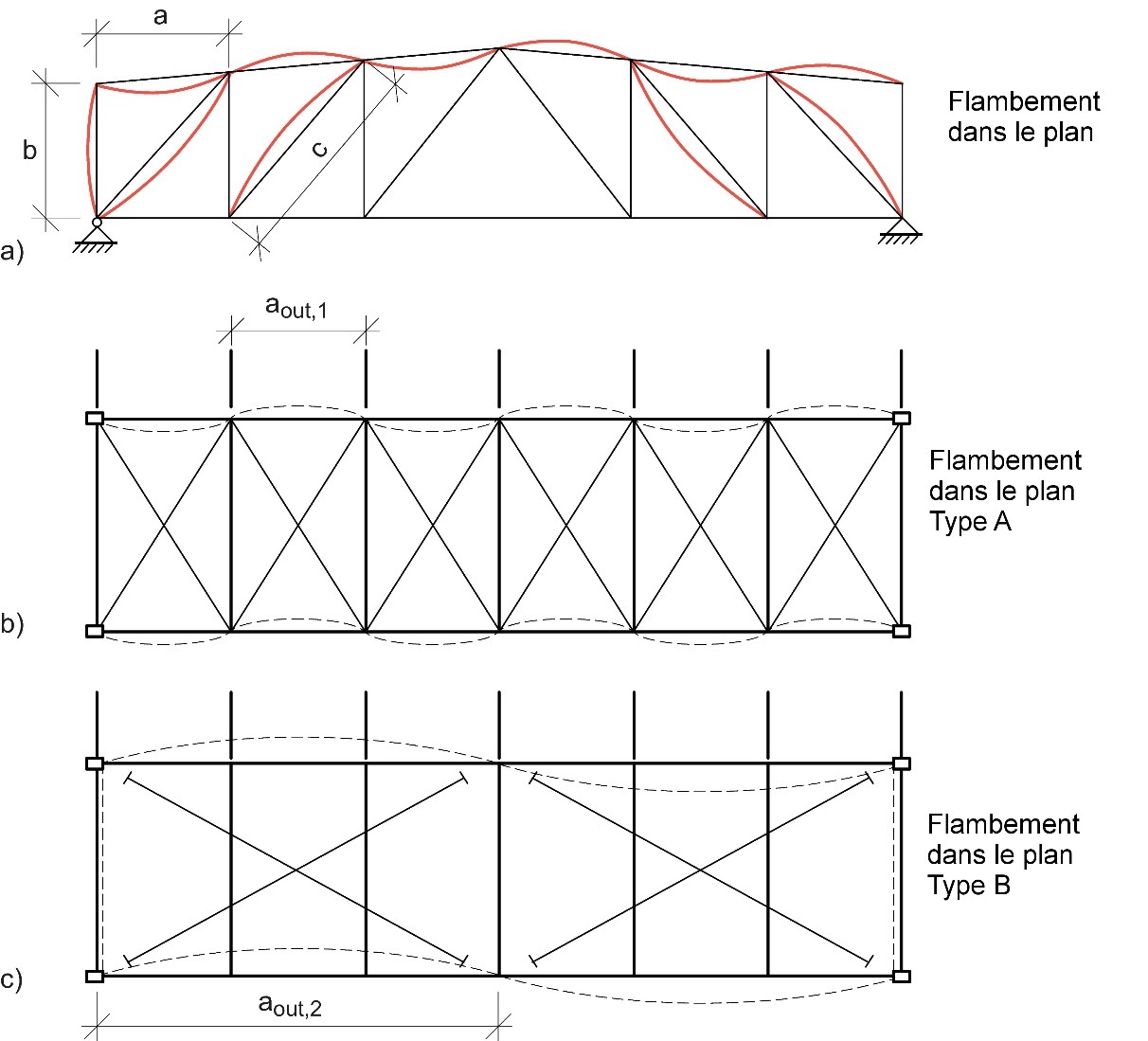
Figure 8.15 : Exemples d'évaluations des longueurs de flambement théoriques dans des poutres à treillis.

Afin de réduire la longueur de flambement hors-plan (si nécessaire), il est possible de contreventer les éléments (cf. Figure 8.15, (b) et (c)). Dans le cas d'un toit comprenant un système de contreventement de type A (Figure 8.15), les points d'appui sont définis par les pannes fixées aux points d'assemblages fixes du contreventement transversal du toit.

Dans le cas d'un toit comprenant un système de contreventement de type B, la membrure supérieure peut flamber hors-plan le long de quelques panneaux composant l’âme de la poutre à treillis. À noter que la membrure inférieure peut également être soumise au flambement, lorsque les forces de soulèvement sous l'action du vent sont supérieures aux charges permanentes.

Tableau 8.1 : longueurs de flambement de barres de treillis. Les symboles sont présentés à la Figure 8-15.

8.4. VERIFICATION DES ETATS LIMITES DE SERVICE

Enfin, il convient de procéder à la vérification de l'état limite de service de la poutre à treillis (cf. Chapitre 6). Il s'agit de vérifier que la flèche maximale induite par les charges de service est inférieure à celle admise par les codes (généralement l/200 et l/300 pour la flèche instantanée et la flèche finale, respectivement). Pour calculer les flèches, on retiendra que le glissement au niveau des assemblages influe grandement sur la flèche totale d'une poutre à treillis. Un tel effet peut être pris en compte de deux manières, à savoir : i) directement, en modélisant les structures avec des ressorts aux nœuds, ii) indirectement, en modélisant la structure avec des articulations aux nœuds, puis en augmentant la flèche obtenue selon un coefficient donné pour prendre en compte le glissement et les rotations au niveau des assemblages. Ce coefficient peut être choisi comme étant égal à 1,3-1,5 pour les nœuds boulonnés (cf. Figure 8.16 a) et égal à 1,1-1,2 pour les nœuds à broches (cf. Figures 8.16 (b) et 8.17).

Si les calculs sont effectués manuellement (et non de manière informatique), l'effet de variations de la longueur d'éléments doit également être pris en compte. En règle générale, la vérification de l'état limite de service dicte rarement la conception de poutres à treillis en bois, compte tenu de la rigidité à la flexion relativement importante de ces structures.

Très souvent, ces poutres sont fabriquées avec une contreflèche (aux membrures supérieure et inférieure). L'amplitude de cette dernière pourra être d'environ l/150 - l/200.

8.5. DETAILS

La qualité, la durabilité et, principalement, les coûts de fabrication des poutres à treillis dépendent dans une large mesure des assemblages utilisés pour les nœuds. Les poutres à treillis sont généralement composées d'un grand nombre de nœuds. C'est pourquoi il est conseillé d'opter pour des solutions de nœuds aux propriétés suivantes :

Croisement des axes des éléments en un seul et même point des nœuds ;
Configuration concentrée, faible extension ;
Assemblage facile et rapide ;
Résistance au feu appropriée (si nécessaire) ;
Nombre d'éléments métalliques limité ;
« Type standard » (possibilité d'utiliser le même type d'assemblage pour le plus grand nombre possible de nœuds de la poutre).

Le calcul et la conception des assemblages sont décrits au Chapitre 14. La section suivante propose une description de certains nœuds couramment utilisés sur des poutres à treillis.

8.5.1. Nœuds d'assemblage des barres de treillis et des membrures

Dans le cas de poutres à treillis possédant des membrures et des barres de treillis simples, les types d'assemblages utilisés aux nœuds consistent en des assemblages à broches ou boulons et à plaques métalliques (cf. également Section 14.9). La Figure 8.16 illustre deux types de nœuds, à savoir (a) à boulons et à plaques métalliques externes, et (b) à broches et à plaques insérées. Les nœuds aux configurations similaires à celle présentée à la Figure 8.16 (b), mais avec plusieurs plaques insérées comme illustré à la Figure 8.17, constituent des solutions idéales pour les poutres à treillis à très grandes portées (entre 70 et 80 m max.) et/ou soumises à des charges lourdes.

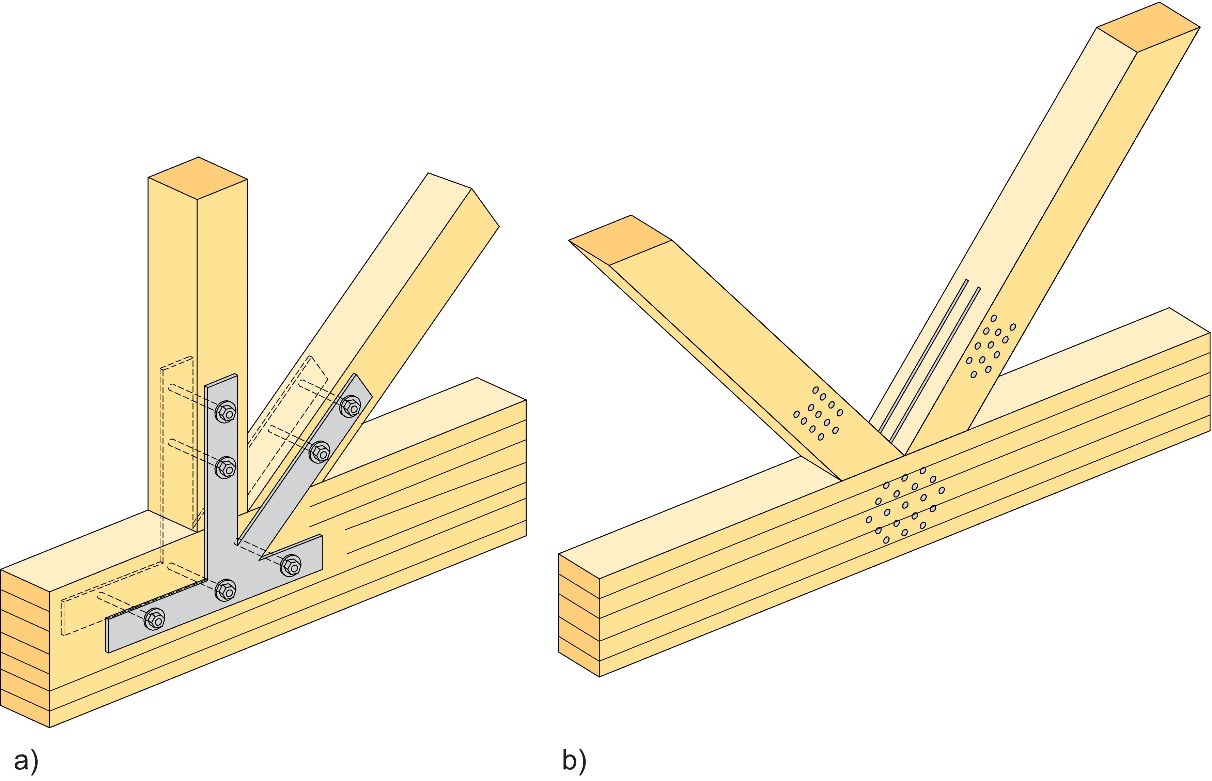
Figure 8.16 : (a) Nœud à boulons et à plaques métalliques externes, et (b) nœud à broches et à plaques insérées.

En France, nombre de grandes poutres à treillis (bâtiments industriels, commerciaux et sportifs, ponts) ont été fabriquées avec des assemblages consistant en des broches et des plaques insérées. Pour ce type d'assemblage, il est devenu pratique courante d'utiliser des plaques insérées d'une épaisseur t = 8 mm et des broches d'un diamètre d = 12 mm. Les éléments métalliques sont fabriqués dans un acier doux courant (par ex. S355). Afin d'optimiser l'assemblage d'un point de vue de la résistance tout en garantissant une ductilité structurelle satisfaisante, l'espacement entre les plaques insérées, l’espacement entre les assembleurs, la distance entre la broche et l'extrémité sollicitée et la distance entre la broche et l'extrémité non sollicitée devront être choisis selon les indications de la Figure 8.17. Une attention spéciale devra être apportée aux éventuelles ruptures par cisaillement de bloc, lesquelles jouent un rôle particulièrement majeur dans le cas où plusieurs plaques insérées sont associées à un grand nombre de broches (cf. Chapitre 14).

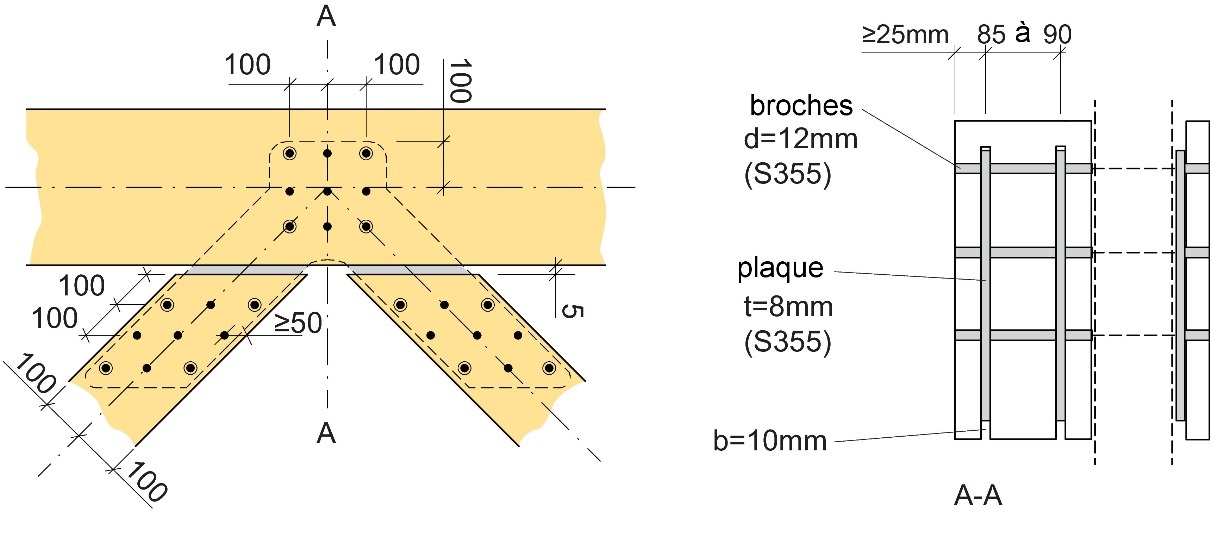
Figure 8.17 : Type de nœud couramment utilisé et indications des espacements.

Les poutres à treillis composées de plusieurs éléments assemblés parallèles (généralement deux ou trois éléments distincts) sont également une pratique courante. Plus la portée et/ou les charges appliquées sont importantes, plus le nombre d'éléments parallèles est élevé. La Figure 8.18 présente plusieurs solutions possibles pour les nœuds. Dans les nœuds illustrés à la Figure 8.18, (a) et (b), les forces entre les diagonales et les membrures sont transmises par le biais d'un seul boulon qui traverse tous les éléments. La transmission des forces entre le boulon et chaque barre de treillis intervient par réaction d’appui entre le boulon et les plaques perforées, plutôt que par appui entre le boulon et le bois (les trous des éléments en bois de la Figure 8.18 (a) sont généralement plus grands que les trous correspondants des plaques perforées). Les plaques perforées, lesquelles sont renforcées autour du trou, sont assemblées aux éléments en bois au moyen de pointes en nombre suffisant pour supporter la charge pour laquelle l'élément est conçu. Dans le nœud illustré à la Figure 8.18 (c), les forces sont transmises entre les membrures et les diagonales tendues d'une manière similaire à celle évoquée pour les cas (a) et (b) de la Figure 8.18. Dans l'assemblage (c), la transmission des forces entre la membrure inférieure et les diagonales comprimées intervient, quant à elle, par réaction d’appui directe bois-bois.

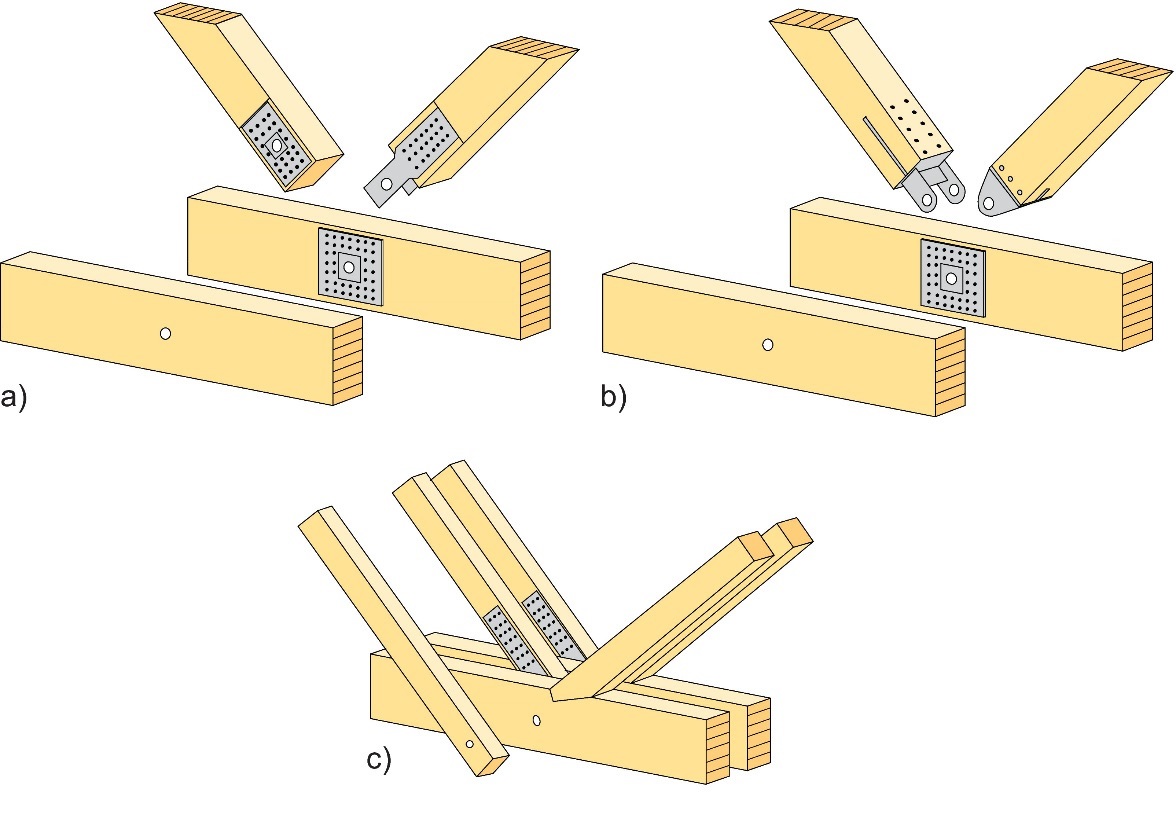
Figure 8.18 : Nœud comprenant (a) des plaques perforées et un boulon / une rotule, (b) des plaques perforées, des plaques insérées et un boulon / une rotule, et (c) identique à (a) pour les diagonales tendues et « assemblage à entaille » (assemblage de charpenterie) pour les diagonales comprimées.

Les poutres à treillis de type Howe (diagonales comprimées) peuvent être conçues avec des tiges métalliques en guise de montants, à condition que la compression n'intervienne pas à cet endroit sous une quelconque charge. Cette solution permet d’éviter les assemblages tendus difficiles. En effet, les assemblages au niveau des extrémités de la tige métallique sont réalisés par simple perçage préalable d'un trou à travers les membrures, après quoi la tige est fixée à son extrémité à l'aide d'un écrou et d’une plaque d'une taille suffisamment grande. La tige est, en principe, légèrement précontrainte. La Figure 8.19 présente une solution possible de nœud.

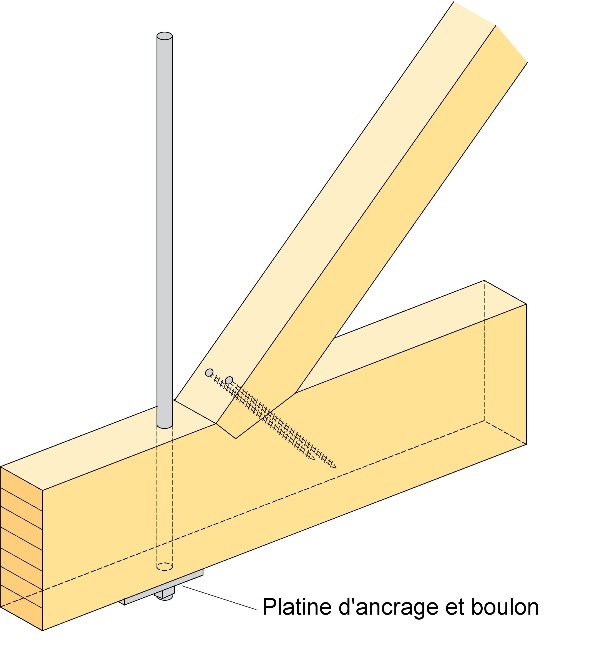
Figure 8.19 : Nœud avec une diagonale en bois comprimée et une tige métallique tendue.

8.5.2. Nœuds au faîtage et aux appuis

La Figure 8.20 illustre deux types de nœuds possibles pour des assemblages de faîtage de fermes. L'assemblage de type (a) peut être réalisé au moyen de goussets en contreplaqué, lamibois (avec placage lamellé-croisé) ou de plaques perforées métalliques. Cette solution est adaptée en cas de charges modérées. La solution (b) consiste en des broches et des plaques métalliques insérées. En ce qui concerne les structures présentant une grande portée et/ou des charges lourdes, il est possible d'utiliser plusieurs plaques insérées afin d'accroître la résistance du nœud.

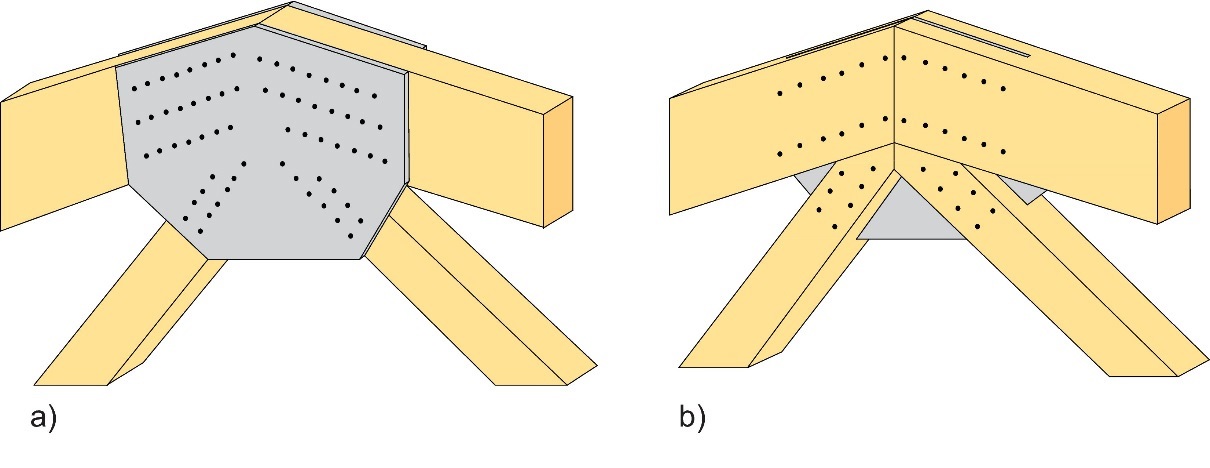
Figure 8.20 : Nœuds au faîtage de fermes : (a) avec goussets en contreplaqué, lamibois ou plaques perforées ; (b) avec broches et plaques insérées.

La Figure 8.21 illustre deux types de nœuds possibles pour des assemblages d’appuis de poutres à treillis. Les deux solutions présentées dans cette figure font appel à des broches et à des plaques insérées. La solution (a) consiste en un nœud dans le cas d'une poutre à treillis à éléments simples, tandis que la solution (b) consiste en un nœud dans le cas d'une poutre à treillis à éléments doubles.

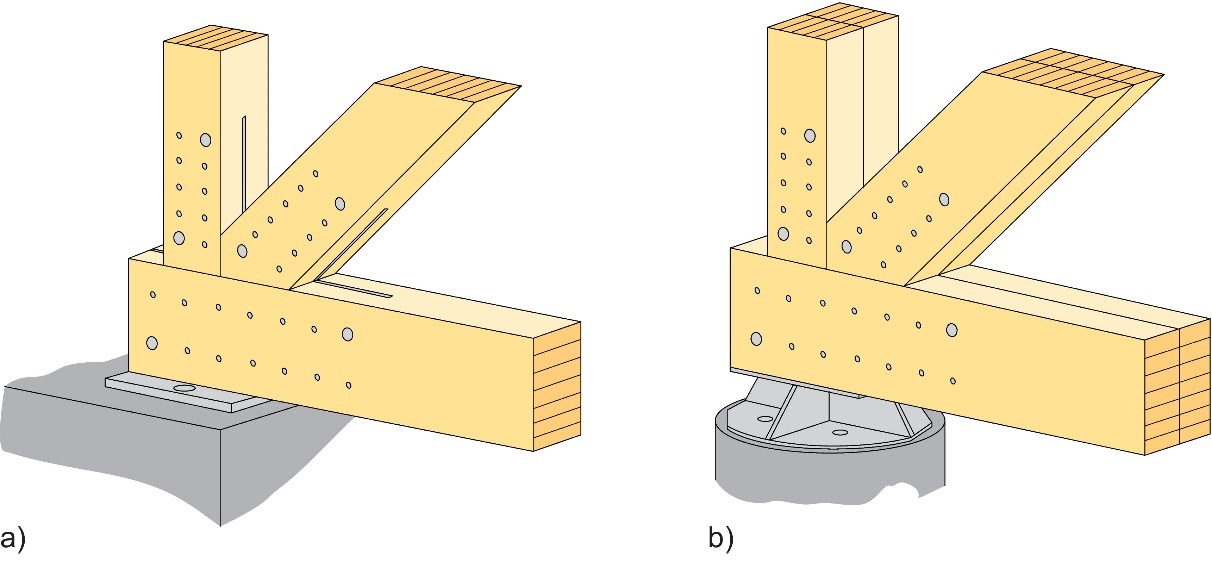
Figure 8.21 : Deux exemples de nœuds à l'appui de poutres à treillis comprenant des broches et des plaques métalliques : (a) poutre à éléments simples ; (b) poutre à éléments doubles.