De nos jours, les portiques en bois sont, presque sans exception, réalisés en lamellé-collé. Les reins sont généralement de forme courbe (lamelles continues), assemblés par entures multiples ou bien reconstitués (cf. Figure 10.1). La forme du portique devra suivre, dans la mesure où les aspects esthétiques et fonctionnels le permettent, le funiculaire de la combinaison de charges principale. Les reins courbes ou reconstitués répondent à cette exigence avec plus de facilité, et sont donc mieux adaptés pour les grandes portées.
La pente du toit devra être d'au moins 14°, notamment dans un souci de réduire la flèche au niveau du faîtage.
Le portique à trois articulations est idéal pour des portées allant jusqu'à 30-40 m. Pour des raisons de transport, la distance (en ligne droite) du pied au faîtage ne devra pas dépasser 24 m, tandis que la distance perpendiculaire entre cette « ligne » et le bord extérieur du rein devra être d'au moins 3,7 m.
Le portique à deux articulations offre une structure, certes, plus résistante, mais qui doit en général être fabriquée et transportée en au moins trois parties, lesquelles sont rigidement assemblées sur place. Des assemblages peuvent être placés aux zones de la structure présentant de faibles moments. Les assemblages rigides impliquent une mise en œuvre plus compliquée que les assemblages articulés, et donc un coût supérieur ; sans oublier leur visibilité souvent très importante et inappropriée. En revanche, les pièces de la structure sont plus petites que celles d'un portique à trois articulations, et donc plus faciles à transporter.
Les portiques sans articulation ne sont généralement pas utilisés pour les structures en bois.
Le portique à trois articulations est sans conteste le type le plus couramment choisi. C'est pourquoi les sections suivantes proposeront simplement des informations concernant la conception de ce type de portique.

Figure 10.1 : Exemples de portiques à trois articulations : a) portique aux reins courbes ; b) portique aux reins assemblés par entures multiples ; c) portique reconstitué (avec jambe de force).
10.1. CALCUL ET CONCEPTION DU PORTIQUE A TROIS ARTICULATIONS
Le portique à trois articulations est stable sous forces horizontales dans son propre plan, et isostatique. En effet, la répartition des moments reste inchangée même si les fondations sont irrégulières ou que des déformations non prévues se produisent dans les assemblages. De plus, ce type de portique est articulé au niveau des fondations, ce qui en simplifie la construction des éléments de base. Si les conditions du sol sont mauvaises, les réactions horizontales au niveau des appuis peuvent être supportées par des éléments tendus situés entre les fondations (dans ou sous la dalle).
Généralement, avec des pentes de toiture d'environ 15°, la combinaison de charges déterminante englobe le poids propre et la neige, auxquels peuvent se rajouter des charges concentrées induites par des ponts-roulants et d’autres systèmes similaires. Cependant, en cas de toitures à forte pente, les combinaisons de charges incluant le vent comme charge principale peuvent revêtir une importance fondamentale.
Les déformations sont généralement calculées à l'aide de programmes informatiques par éléments finis.
10.2. FORCES INTERNES ET REACTIONS D’APPUI
Le portique à trois articulations est isostatique. Par conséquent, les forces internes intervenant dans une section transversale peuvent être déterminées à l'aide d'équations d'équilibre. Cependant, la forme géométrique implique des calculs complexes. Ces derniers peuvent être adéquatement réalisés à l'aide d'un logiciel de calcul.
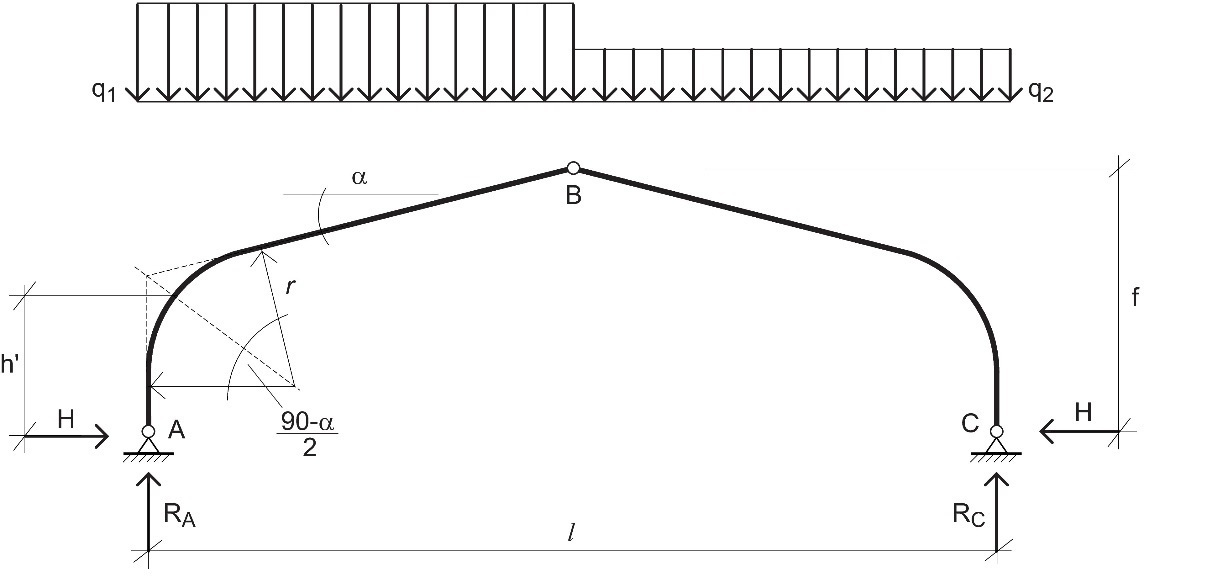
Figure 10.2 : Portique à trois articulations aux reins courbes. Symboles.
Dans des conditions de charge asymétrique uniformément répartie (cf. Figure 10.2), les forces de réaction et internes agissant dans un portique à trois articulations peuvent être calculées à l’aide des expressions suivantes :

À noter que si le portique comporte un élément vertical au niveau de l'appui (par ex. reins assemblés par entures multiples), le rayon de courbure r peut être défini comme étant égal à zéro. Dans ce cas, le moment de flexion au rein (cf. Éq. 10.5) devient donc simplement M=H·h.
10.3. METHODE DE CALCUL
Le calcul peut être réalisé selon la méthode détaillée ci-dessous :
1 Déterminer les principales dimensions et les valeurs de calcul des descentes des charges climatiques et des charges applicables.
2 Schématiser les axes centraux approximatifs du portique selon la figure ciaprès fondée sur l'expérience :
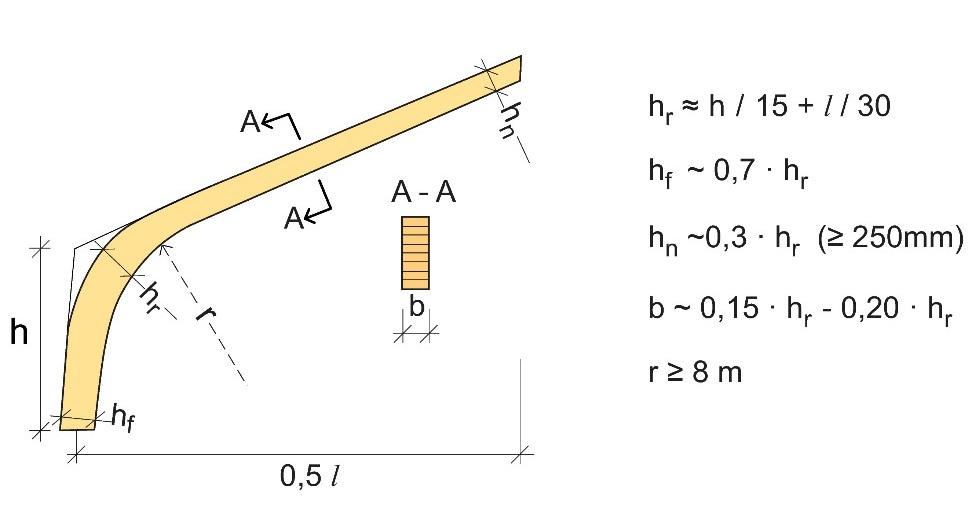
Figure 10.3 : Dimensionnement préliminaire d'un portique lamellé-collé.
3 Calculer les réactions d'appui et les forces internes au pied et au faîtage pour différentes combinaisons de charges.
4 Déterminer les dimensions de la section transversale requise au pied selon l'effort normal maximal ou l’effort tranchant maximal.
5 Déterminer les dimensions de la section transversale requise au faîtage selon les mêmes critères que ceux utilisés pour le pied. Le calcul de l'élément de fixation du faîtage peut également influer sur les dimensions de la section transversale.
6 Rectifier le schéma réalisé au point 2 et déterminer le moment de flexion et les forces internes au rein pour différentes combinaisons de charges.
7 Déterminer les dimensions transversales requises au rein au regard (a) de la stabilité et (b) de la conception des détails conformément aux instructions données aux Sections 10.4 et 10.6.
8 Vérifier les valeurs de compression et de flexion simultanée de la traverse conformément aux instructions de la Section 10.4. En principe, la hauteur de la section transversale varie de façon linéaire entre le faîtage et le rein. Les sections transversales critiques ne correspondent donc pas à la section soumise au moment positif maximal. Dans la plupart des cas, une simple vérification de quelques sections transversales choisies au hasard suffit.
Vérifier l'état limite de service conformément aux instructions de la Section 10.5.
10.4. VERIFICATION DE LA STABILITE
Qu'il s'agisse de portiques, de poteaux ou de poutres, la résistance au flambement autour du grand axe et du petit axe (de la section transversale lamellée-collée) doit faire l'objet d'une vérification de la stabilité. Compte tenu de la déformabilité des assemblages et des conditions d'appui généralement défavorables, la longueur de flambement ne peut être évaluée que de façon approximative.
Le flambement latéral est vérifié dans les portiques de la même manière que tout poteaupoutre entre des maintiens latéraux (contreventements). À noter que la longueur de flambement dépend du système de contreventement choisi et, dans une certaine mesure, de la toiture. Par exemple, si un système de plaques continues suffisamment rigides est utilisé, aucun flambement hors-plan ne se produira. Par contre, un flambement latéral interviendra entre les points de fixation des pannes aux traverses (longueur de flambement : a1 - cf. Figure 10.4). En revanche, si ce système n’est pas suffisamment rigide, la longueur de flambement à adopter dans le cadre du calcul devra correspondre à la distance entre les nœuds de l’armature de contreventement (longueur de flambement : a - cf. Figure 10.4).
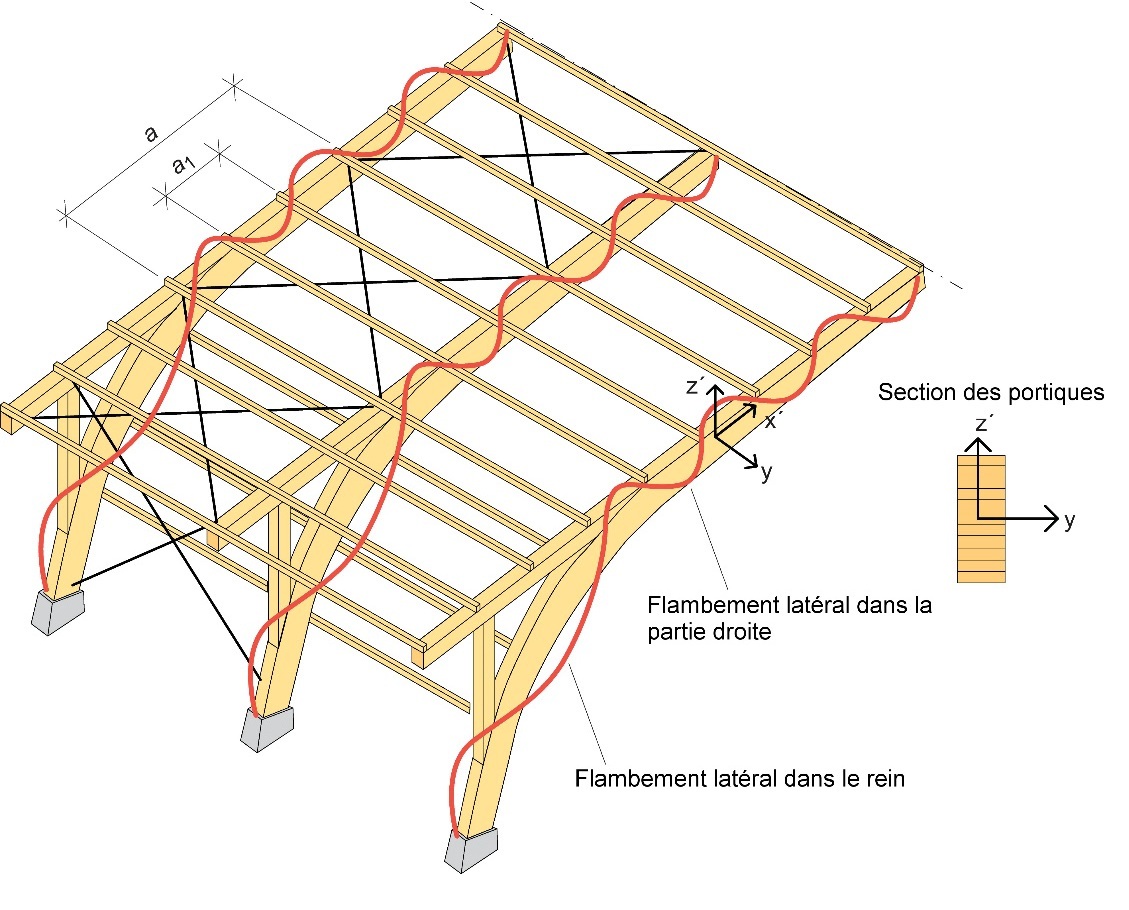
Figure 10.4 : Flambement latéral du portique et du rein. La toiture consiste en des tôles rigides (par ex. tôles métalliques ondulées [non représentées sur la figure]).
10.4.1.1. Flambement hors-plan d'éléments linéaires
Le flambement hors-plan doit faire l'objet d'une vérification dans les zones non renforcées, comme des poteaux-poutres, selon le modèle présenté à la Figure 10.5.
Le critère de dimensionnement est formulé comme suit :
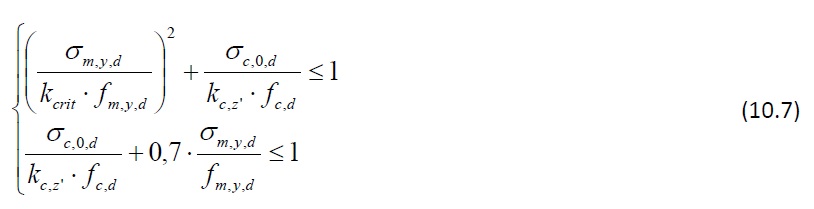
où :
σc,0,d correspond à la contrainte de compression de calcul.
σm,y,d correspond à la contrainte de flexion de calcul selon l’axe y.
fc,d correspond à la résistance de calcul à la compression.
fm,y,d correspond à la résistance de calcul à la flexion selon l’axe y.
kc,z’ désigne le coefficient de réduction associé au flambement hors-plan (c'est-à-dire flambement selon l’axe z ; cf. Figure 10.4).
kcrit désigne le coefficient de réduction associé au déversement (cf. Section 4.1.3).
Pour plus de détails concernant les symboles utilisés, se référer également au Chapitre 4.
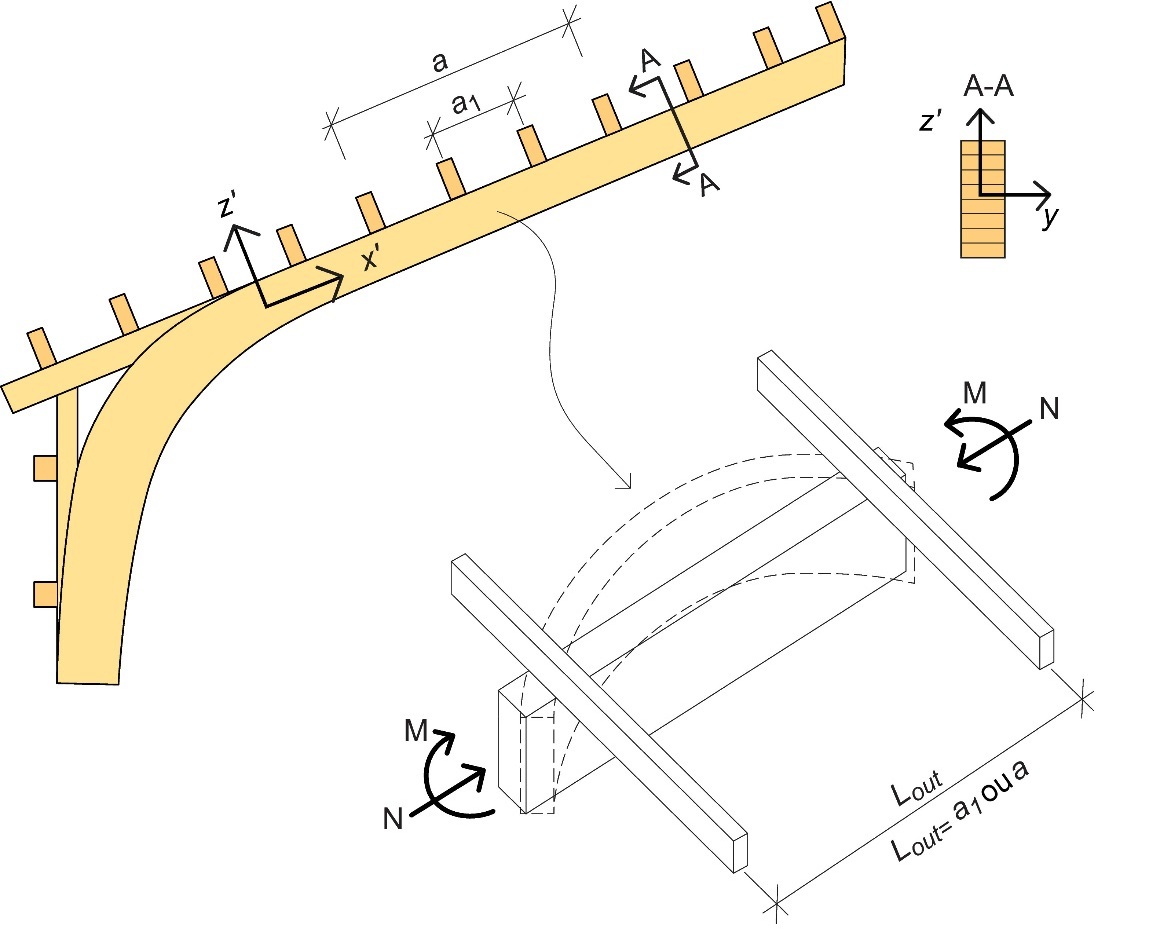
Figure 10.5 : Modèle de vérification du flambement hors-plan de l'élément linéaire du portique. Si le matériau de couverture est suffisamment rigide, la longueur de flambement peut être présumée égale à a1. Autrement, il conviendra de supposer une longueur de flambement égale à a (cf. également Figure 10-4).
10.4.1.2. Flambement hors-plan d'éléments courbes
En principe, les portiques ne présentent aucun renforcement dans la zone des reins. Les charges de gravité induisent des moments de flexion négatifs aux reins, provoquant une compression sous la section transversale. De plus, des contraintes de compression sous effort normal sont également présentes dans cette zone. C'est pourquoi il convient de vérifier l'action combinée des forces de compression et de flexion au niveau des reins.
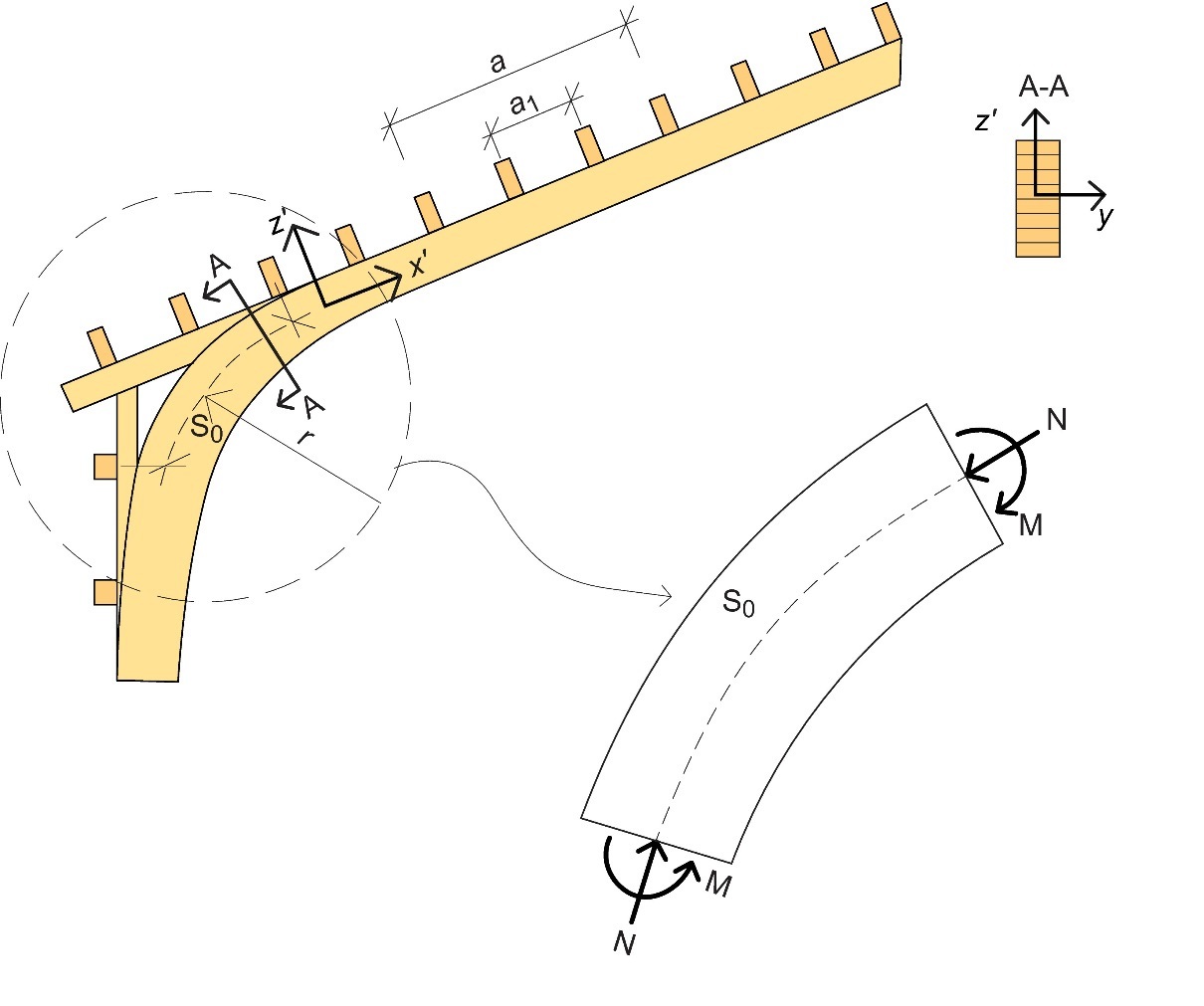
Figure 10.6 : Modèle de vérification du flambement hors-plan du rein.
Les conditions de calcul à satisfaire sont similaires à celles applicables à l'élément linéaire (cf. Éq. 10.7), à l'exception du coefficient kr (cf. Chapitre 7), lequel est intégré afin de tenir compte de la réduction de résistance due à la flexion des lamelles au cours de la production.
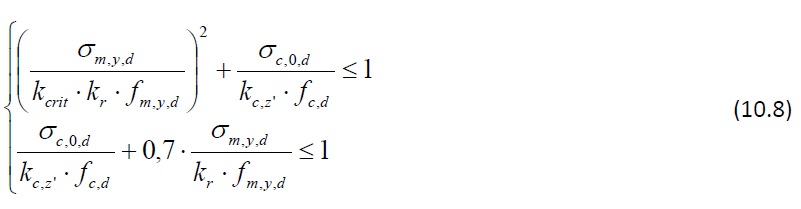
Pour calculer le moment de flexion critique Mcr à utiliser pour déterminer le rapport d'élancement correspondant et, enfin, le coefficient de réduction kcrit (cf. Chapitre 4, Section 4.1.3), la formule suivante devra être appliquée :

À noter que pour r→∞, l'Éq. 10.9 devient identique à celle permettant de déterminer le moment critique des éléments linéaires soumis à un moment de flexion constant (cf. Chapitre 4).
10.4.2. Flambement dans le plan (flambement autour du grand axe)
Le flambement dans le plan du portique est généralement plus compliqué que celui des éléments de poteaux-poutres courants. La méthode commune d'analyse applicable aux portiques et aux arcs consiste en deux étapes :
1. Analyse de flambement linéaire
2. Analyse au second ordre
10.4.2.1. Analyse de flambement linéaire
Dans le cas d'une analyse de flambement linéaire, les portiques et les arcs peuvent faire l'objet d'une vérification semblable à celle de poteaux-poutres (à savoir éléments soumis simultanément à des forces de flexion et de compression). Les contraintes induites par des charges externes sont calculées selon une théorie élastique linéaire considérant l'équilibre du système statique non déformé. Les contraintes provoquées par des imperfections latérales et dans le plan et les flèches induites sont prises en compte en multipliant les valeurs de résistance en flexion et en compression par les coefficients de réduction pour le flambement kc et kcrit. Ici, kc désigne le coefficient de réduction associé au flambement sous compression axiale. Dans le cas de rapports de flèche normaux, le premier mode de flambement d’un portique est en principe asymétrique et de forme similaire à celle illustrée à la Figure 10.7.
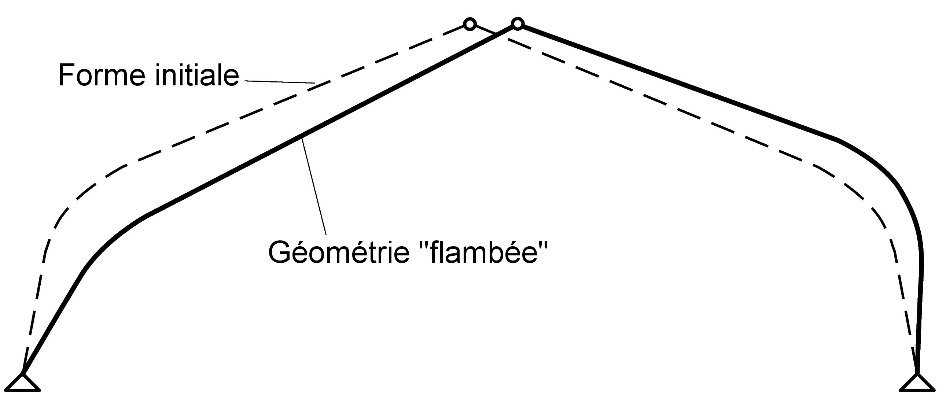
Figure 10.7 : Flambement dans le plan d'un portique à trois articulations.
Pour déterminer la charge de flambement selon l'analyse simplifiée, la longueur de flambement Le est nécessaire. Cette longueur peut être obtenue de deux manières : a) numériquement, dans le cadre d'une analyse de flambement linéaire à l'aide d'un programme par éléments finis, ou b) par formules empiriques.
En première approximation, la longueur de flambement du portique peut être considérée comme étant égale à :

où ahf désigne la longueur du demi-portique (cf. Figure 10.8).
Pour une analyse plus affinée, il est possible d'utiliser la formule donnée par l’ancien code allemand concernant les structures en bois (DIN 1052), à savoir :

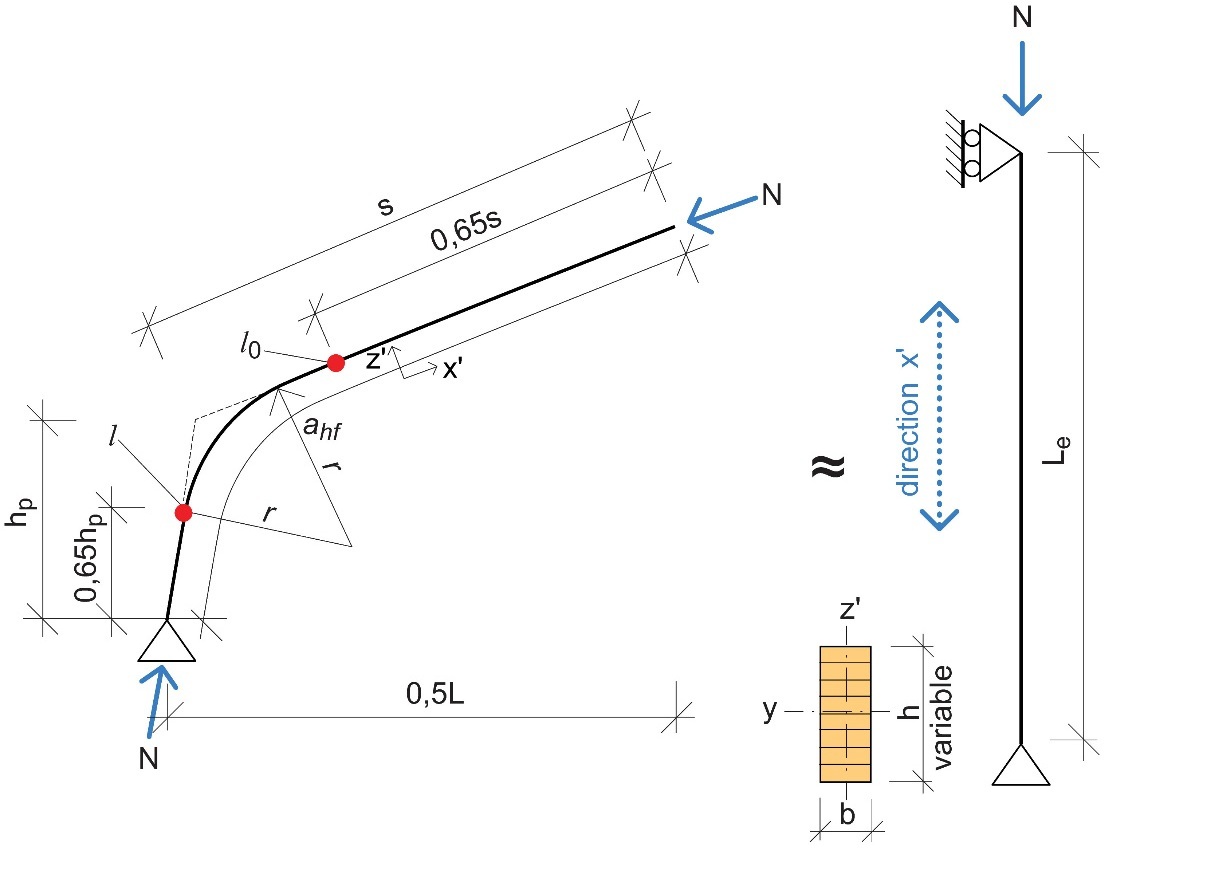
Figure 10.8 : Modèle de détermination de la longueur de flambement dans le plan d'un portique à trois articulations.
Le critère de dimensionnement est formulé comme suit :

où :
kc,y désigne le coefficient de réduction associé au flambement dans le plan (c'est-à-dire flambement selon l’axe y; cf. Figure 10.8) ;
les autres symboles sont définis à l'Éq. 10.7 et aux Chapitres 4 et 7.
10.4.2.2. Analyse au second ordre
Dans le cas d'une analyse au second ordre, les contraintes sont calculées selon une théorie non linéaire géométrique considérant l'équilibre du système statique déformé.
Dans ce type d'analyse, les charges de calcul sont appliquées graduellement (par incréments). Avant qu'une charge incrémentale ne soit appliquée à la structure, les déplacements induits par les charges préalables sont calculés. Des charges incrémentales sont appliquées en des endroits déterminés après ajout des déplacements induits par les charges préalables. De cette manière, l'impact de l'ensemble des déplacements (y compris déplacement latéral) induits par les charges préalables sur les forces internes est pris en compte dans le cadre de l'analyse au second ordre. Ce type d'analyse est réalisé à l'aide de logiciels informatiques adéquats par éléments finis.
Si des imperfections géométriques sont également modélisées, les forces internes données par l'analyse au second ordre peuvent être directement utilisées pour dimensionner les éléments, sans réduction de la résistance de calcul liée au flambement (à savoir kc,y=1,0). Il conviendra de supposer que les déformations initiales sont affines à la forme de la déformation sous charge, laquelle pourra être considérée comme une déformation initiale obtenue en appliquant les déviations initiales dans la géométrie comme illustré à la Figure 10.9. La Section 5.4.4 de l'Eurocode 5 propose des recommandations concernant l'amplitude des déviations initiales dans la géométrie de portiques.
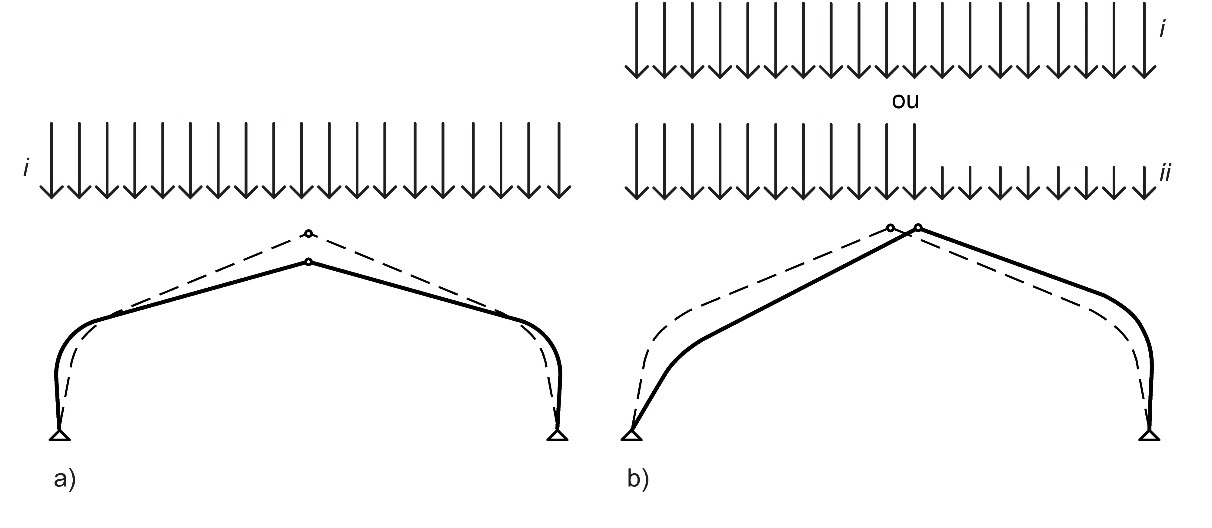
Figure 10.9 : Déviation initiale dans la géométrie et charges correspondantes à adopter pour les analyses au second ordre : (a) flambement symétrique ; (b) flambement (ou mode de déplacement latéral) asymétrique.
10.5. VERIFICATION DE L’ETAT LIMITE DE SERVICE
En principe, les éléments de portiques à trois articulations ne sont pas renforcés. Cependant, dans certains cas (par ex. lorsque des flèches dues à des variations de la teneur en humidité sont anticipées), une contre-flèche peut s'avérer nécessaire.
La vérification de l'état limite de service est réalisée en calculant la flèche au faîtage. Ce calcul peut être effectué le plus simplement possible à l'aide de certains programmes fiables par éléments finis disponibles sur le marché.
Le code du bâtiment ne formule aucune recommandation quant à des limites de flèche, étant donné que ces limites dépendent de l'utilisation prévue de la structure. Cependant, la flèche finale induite par le poids propre et la charge variable applicable (notamment effet de fluage) ne devra en aucun cas dépasser 1/200 de la portée.
10.6. CALCUL DES REINS
10.6.1. Reins courbes
Les reins courbes consistent généralement en une section transversale constante avec, parfois, un coin d’angle extérieur, comme illustré à la Figure 10.10. Afin de faciliter les opérations de fabrication tout en évitant de réduire la résistance, le rapport choisi entre le rayon de courbure et l'épaisseur des lamelles est souvent relativement grand (r/t≈240). Une épaisseur de lamelle t = 33 mm et un rayon de courbure r = 8 m sont couramment utilisés pour fabriquer des portiques aux reins courbes. Le coin d’angle (à l'extérieur de la ligne pointillée sur la figure) peut alors soit agir conjointement avec la section transversale (action combinée si le coin est collé), soit être simplement cloué ou vissé. Il convient de vérifier les contraintes radiales de traction (contraintes perpendiculaires au fil) dans les cas où des combinaisons de charges induisent des moments positifs (bord intérieur tendu) au niveau du rein - notamment lorsque la charge de vent constitue la composante principale d'une combinaison de charges. Les reins lamellés-collés sont essentiellement dimensionnés de la même manière que pour une poutre banane (cf. Chapitre 7).
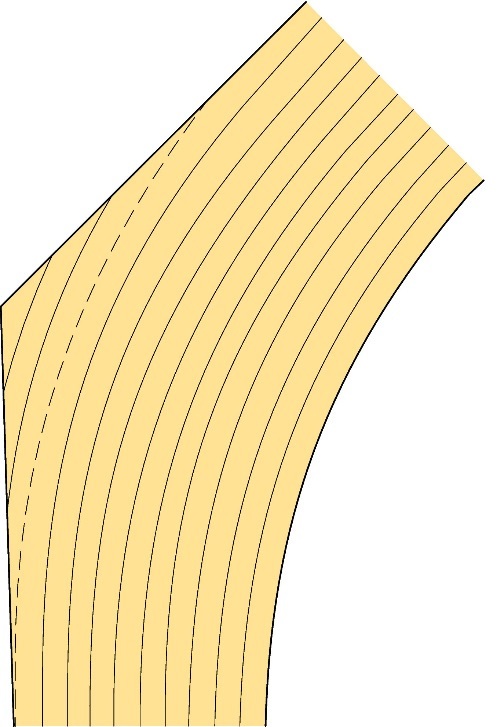
Figure 10.10 : Rein courbe avec une pièce d’angle entièrement collée.
10.6.2. Reins assemblés par entures multiples
Les reins assemblés par entures multiples sont généralement fabriqués avec une pièce d'assemblage (cf. Figure 10.11). Cette pièce a pour principale fonction de réduire l'angle entre la force axiale et le fil dans la zone du coin, et donc de favoriser la capacité résistante du rein. Dans les cas normaux, c’est-à-dire lorsque la combinaison de charges déterminante génèrera un moment négatif au rein, les lamelles de la traverse et du montant devront être parallèles à la partie supérieure du portique (cf. Figure 10.11). Les lamelles de la pièce d'assemblage du rein sont généralement dans tous les cas parallèles à la partie inférieure du portique.
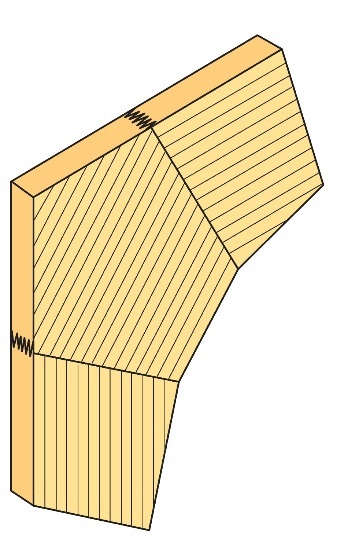
Figure 10.11 : Rein assemblé par entures multiples avec la pièce d'assemblage.
Les deux points d'assemblage au rein sont vérifiés selon la méthode semi-empirique suivante :
- Le moment de flexion Mjoint et l'effort longitudinal Njoint perpendiculaire au point d'assemblage sont calculés au milieu de chaque point d'assemblage ;
- L’aire de la section transversale efficace et le module de section efficace aux points d'assemblage sont calculés. Les expressions suivantes (avec les symboles de la Figure 10.12) s'appliquent :
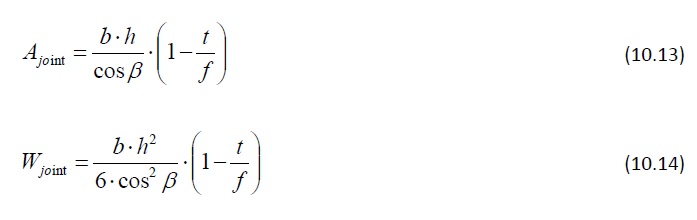
où :
t désigne la largeur du bout de dent des entures.
f désigne le pas des entures de centre à centre à la base.
Le rapport t/f est en principe compris entre 0,1 et 0,2. Par conséquent, si la géométrie de l'assemblage par entures multiples n'est a priori pas connue, les termes entre parenthèses des Éq. 10.13 et 10.14 peuvent être remplacés par 0,8.
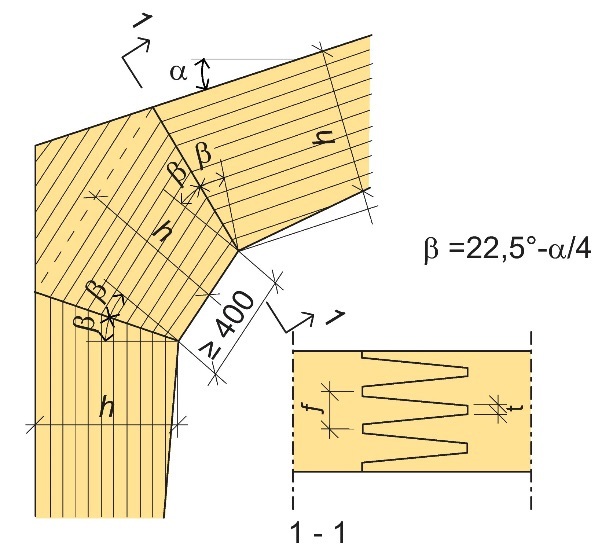
Figure 10.12 : Rein assemblé par entures multiples avec la pièce d'assemblage, symboles et géométrie.
- La valeur de calcul de la résistance à la compression fc,α est déterminée à partir de l'angle β entre les efforts longitudinaux et le fil (cf. Chapitre 4).
- En ce qui concerne les combinaisons de charges générant une force de compression au bord intérieur du rein, la condition critique suivante s'applique :

- En ce qui concerne les combinaisons de charges générant une force de traction au bord intérieur du rein (généralement celles incluant le vent comme charge principale), la condition de calcul suivante s'applique :

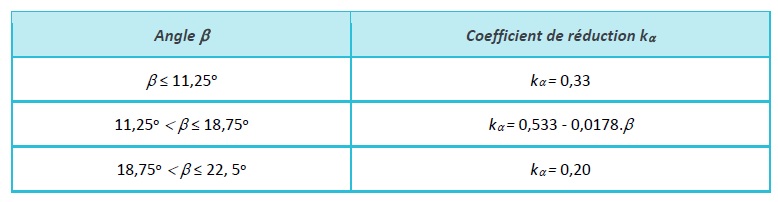
où le coefficient kα dépend de l'angle β entre l'effort longitudinal et le sens du fil de la pièce d'assemblage (cf. Tableau 10.1).
Tableau 10.1 : Coefficient de réduction k
10.6.3. Reins de portiques reconstitués
Les reins reconstitués peuvent être fabriqués de différentes manières. Dans les portiques à jambe de force (Figure 10.13), la section A doit faire l'objet d'une vérification des forces de compression et de flexion simultanées, comme évoqué à la Section 10.6.2, en réduisant éventuellement les valeurs de calcul de la résistance à la flexion et à la compression du fait du déversement et du flambement du portique dans le plan. Par ailleurs, il convient de vérifier les contraintes de cisaillement à la section B.
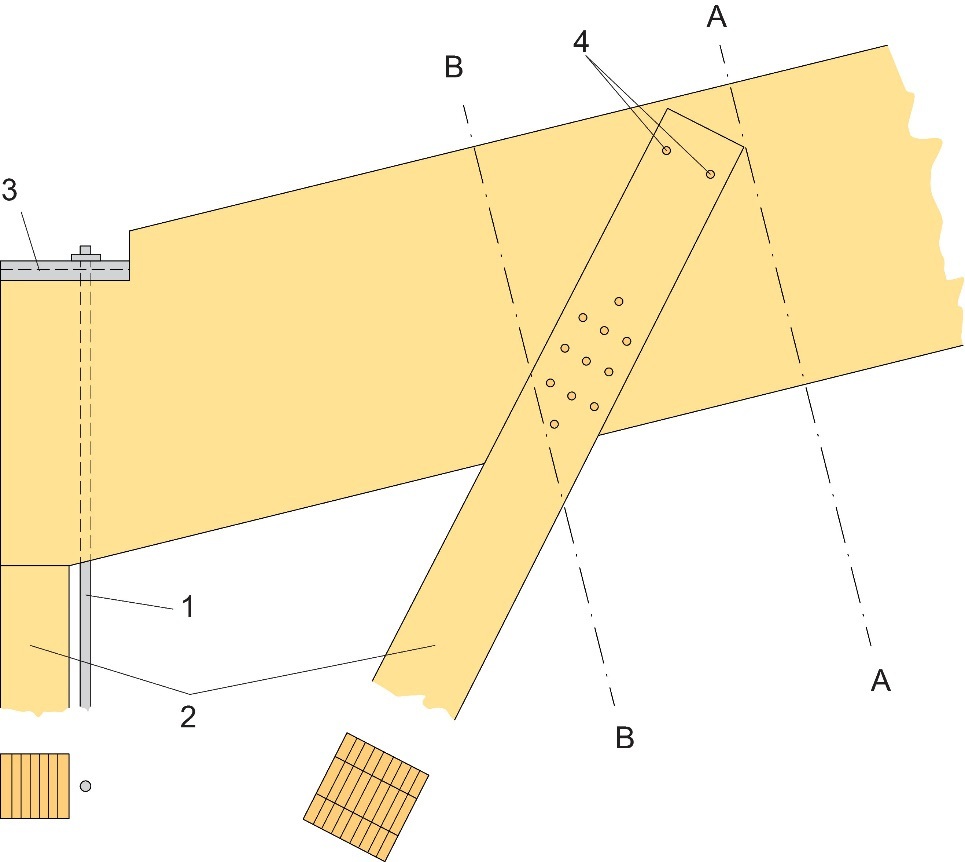
Figure 10.13 : Rein reconstitué avec assemblage boulonné entre la traverse et le montant intérieur : (1) barre tendue en acier, (2) barre comprimée en bois, (3) profilé en U en acier, (4) trous de boulonnage oblongs.
Le montant extérieur est en principe conçu pour supporter des charges axiales, éventuellement associées à des moments simultanés induits par la charge de vent. En cas de charges de gravité prédominantes, des forces de traction importantes interviendront dans le montant extérieur. Ces forces peuvent être transférées vers les fondations au moyen d'une barre tendue en acier (Figure 10.13), tandis que les forces de compression et les moments peuvent être transférés vers le haut avec une simple contrefiche en bois. La barre tendue devra être fixée en haut de la traverse plutôt qu'en bas, afin de limiter au minimum le risque de fissuration.
Le montant intérieur s’apparente à un poteau travaillant en compression et, éventuellement, en flexion, si l'assemblage entre le montant et la traverse est de nature à générer des charges décentrées. L'assemblage entre la traverse et les montants est conçu de sorte que le transfert des forces de compression intervienne principalement au bord inférieur de la traverse, de préférence par pression de contact, au moyen, notamment, d'un tasseau en bois collée dessous la traverse (Figure 10.14). Au niveau de la zone de contact, il existe, cependant, un risque de pénétration des surfaces de contact, d’une manière sensiblement comparable à deux brosses dures pressées l'une contre l'autre. Afin d'éviter ce problème, il peut être approprié de fabriquer l'assemblage en insérant, par exemple, une plaque d'acier. Il est également suggéré d'insérer une ou plusieurs vis entièrement filetées perpendiculairement à la ligne de contact entre le tasseau et la traverse, afin de supporter d'éventuelles forces de traction induites, notamment, par un défaut d’ajustement probable des surfaces de contact.
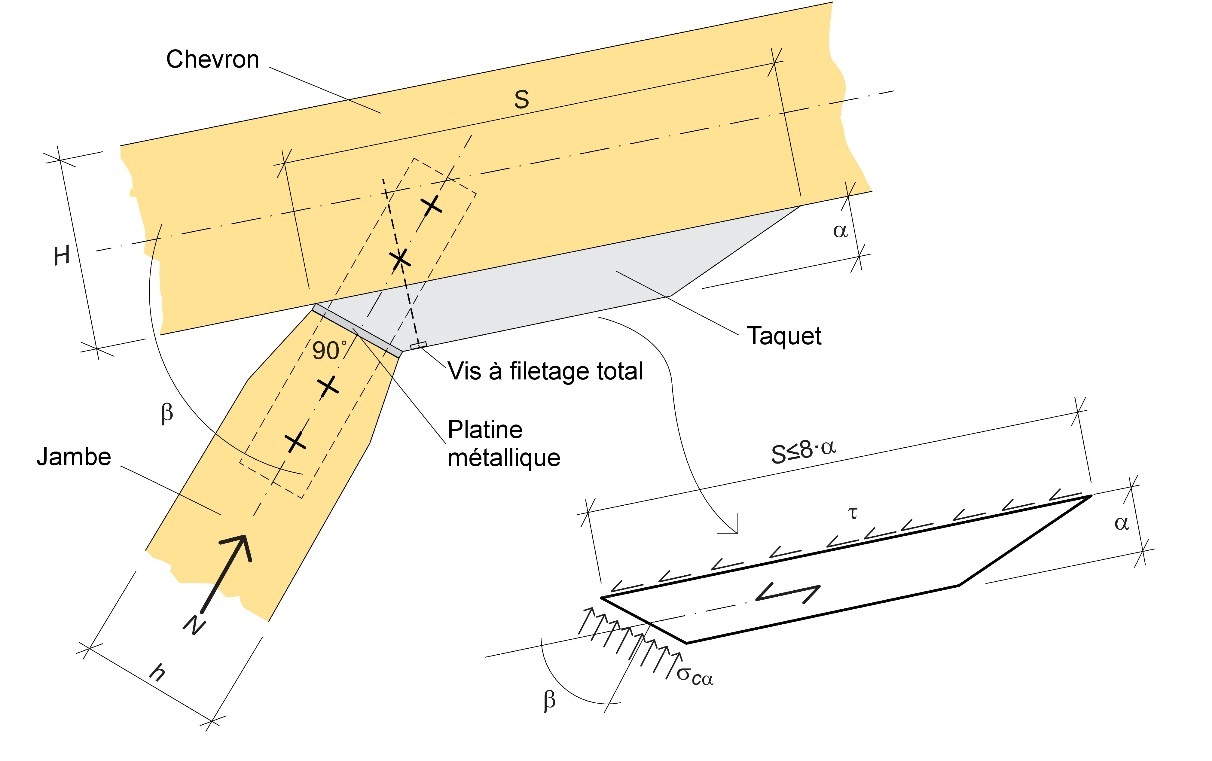
Figure 10.14 : Assemblage de portique : répartition des forces et symboles. L'angle β entre la traverse et le montant est en principe compris dans une fourchette allant de 45o à 60o .
La vérification de l'assemblage peut se dérouler comme suit :
- Vérifier la pression de contact σc,
,d entre le montant et le taquet lamellé-collé :

où fc,


- Vérifier la contrainte de cisaillement entre le taquet et la traverse :

où fv,d désigne la résistance au cisaillement du lamellé-collé (dans l'Éq. 10.18, fv,d est réduite selon un coefficient de 0,5 suivant les résultats expérimentaux).
De plus, il convient de vérifier que la longueur du taquet s soit d'au moins 200 mm et que le rapport entre la longueur du taquet et sa hauteur soit au moins égal à 6 (s/a ≥6).
Il est impossible d’utiliser une longueur supérieure à s = 8 a (en d’autres termes, si s ≥ 8·a, la valeur d'entrée pour s dans l'Éq. 10.18 doit être égale à 8 a).
10.7. DETAILS
10.7.1. Détail de la base articulée de portiques aux reins courbes et assemblés par entures multiples
Les assemblages aux appuis des portiques consistent en des articulations presque sans moment. Selon le type d'assemblage choisi, des moments relativement faibles sont susceptibles d'être transférés. Leur amplitude est cependant limitée à un point tel qu'il est inutile d'en tenir compte lors du dimensionnement du portique. En revanche, ces moments revêtiront une certaine importance pour le dimensionnement de l'assemblage et de l'ancrage.
Outre les rotations autour de l'axe fort, l'assemblage doit également pouvoir transférer les forces verticales et horizontales (cf. Figure 10.15).
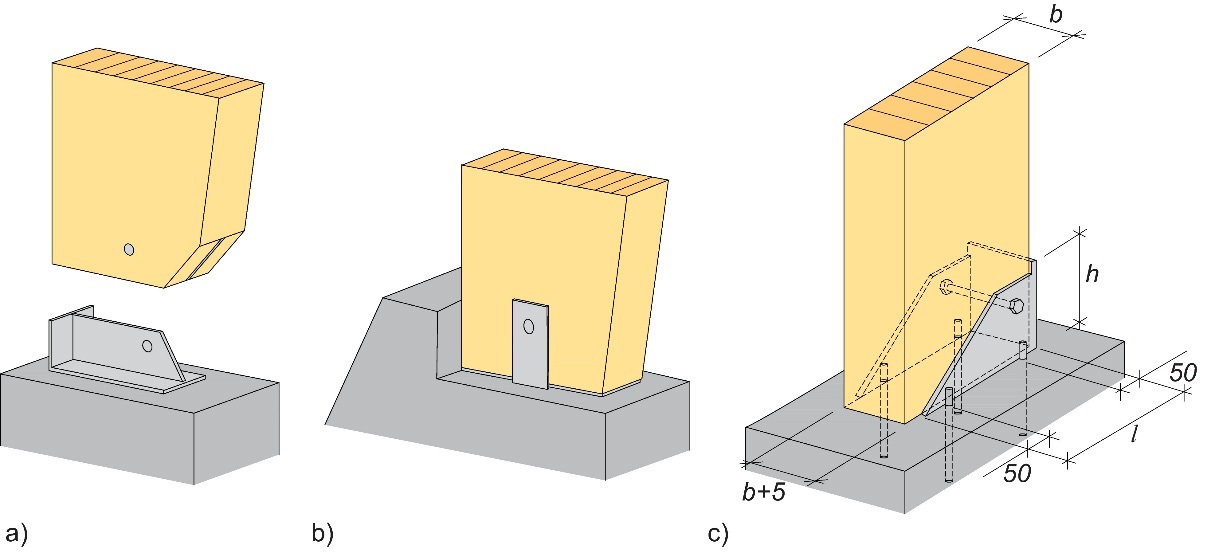
Figure 10.15 : Détails possibles pour la base de portiques aux reins courbes et assemblés par entures multiples : (a) plaque en acier insérée et plaque arrière ; (b) plaques en acier latérales et culée en béton ; (c) plaques latérales et plaque arrière.
Il convient de rappeler le caractère essentiel de tolérances de construction lors de la réalisation de bases en béton avec des pièces en acier coulé (cf. notamment Figure 10.15 (c)). Il est systématiquement recommandé d'utiliser une barrière anti humidité au niveau de la partie inférieure de l'élément en bois (également pour les classes de service 1 et 2), afin d'éviter tout transfert d'humidité dans le bois de bout
10.7.2. Assemblage de faîtage articulé
Les assemblages de faîtage articulés transfèrent des forces horizontales et verticales. Étant donné que les moments ne sont transférés que de manière limitée, ils ne sont pas pris en compte dans le cadre du calcul. L'assemblage devra permettre des variations d'angle des poutres. Si ce mouvement est impossible, d'autres contraintes interviendront, susceptibles de provoquer des dommages non prévus à la structure.
L'assemblage peut être conçu d'une façon similaire à celle de l'assemblage de faîtage de structures à trois articulations (cf. Chapitre 9). Des alternatives possibles sont illustrées à la Figure 10.16.
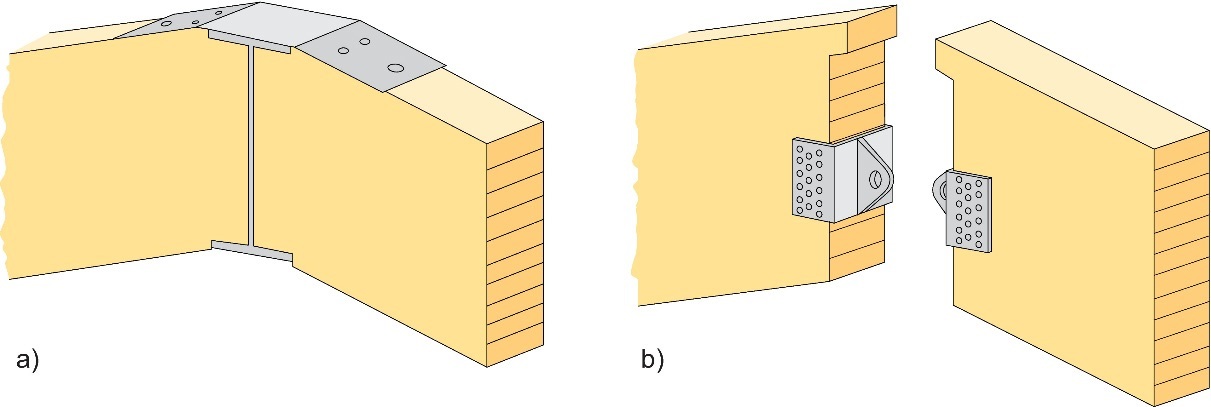
Figure 10.16 : Assemblage de faîtage articulé : (a) éléments entaillés pour accueillir une section en I et plaque supérieure pour résister aux forces de traction ; (b) rotule. La partie supérieure du type d'assemblage (b) devra inclure un jeu pour permettre une libre rotation.
10.7.3. Détails de structures reconstituées
La Figure 10.17 montre certaines solutions possibles pour l'appui en pied et pour l'assemblage entre le tirant métallique et la traverse.
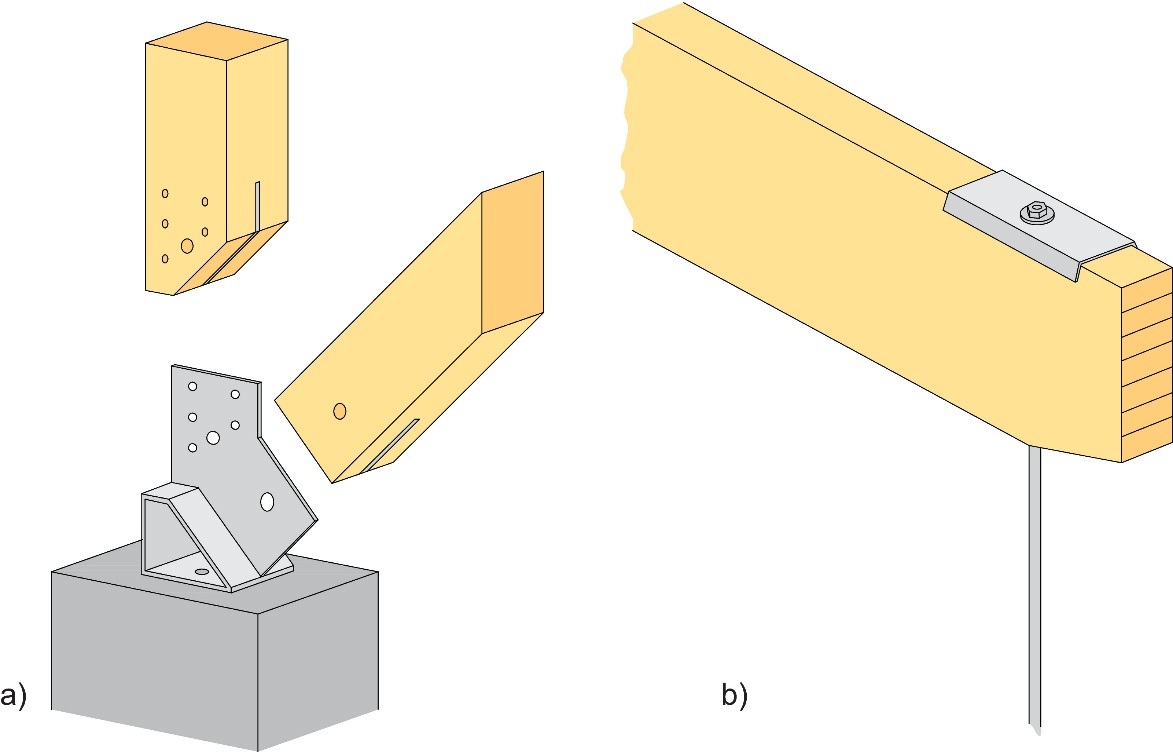
Figure 10.17 : Exemple de détails de portiques reconstitués : (a) appui en pied ; (b) assemblage entre la barre tendue en acier et la traverse.

