VOLUME 2 - 2. MÉTHODES DE CALCUL DES STRUCTURES EN BOIS ET EN LAMELLÉ-COLLÉ

2.1. INTRODUCTION GENERALE AU CALCUL DE STRUCTURE

Le calcul des structures implique de choisir les dimensions des membres porteurs de façon à minimiser le risque qu’une défaillance de la structure provoque des lésions corporelles graves et à garantir que le bâtiment remplit correctement ses fonctions dans des conditions d’utilisation normale, c’est-à-dire en service. La structure porteuse doit être conçue en fonction des exigences définies concernant la résistance, les performances et la durabilité du matériau pendant toute la durée de vie de la structure. Le calcul des structures repose sur la vérification. L’objectif de cette dernière est de démontrer que les exigences définies concernant le matériau, les dimensions et le système structural choisis sont respectées. La vérification peut prendre la forme de calculs ou d’essais ou supposer une combinaison des deux. La durée de service correspond à la période pendant laquelle une structure est destinée à être utilisée aux fins prévues, grâce aux opérations d’entretien planifiées, mais sans qu’aucune réparation d’importance soit nécessaire. La durée de service recommandée pour les bâtiments est généralement de 50 ans et celle des ponts de 100 ans.

2.1.1. Processus de conception et calcul préliminaire

L’étude de conception constitue la première étape d’un projet de construction. Elle consiste à identifier et à examiner les besoins, à définir les exigences relatives aux solutions potentielles, à évaluer et à approuver les solutions potentielles et à développer un concept structural approprié en vue de la conception ultérieure. Une fois le concept choisi, défini et approuvé, la deuxième étape du processus de conception consiste à effectuer une vérification conformément au code de conception normatif. La phase intuitive, qui fait partie de la première étape, inclut la définition des objectifs propres au projet, la compréhension des souhaits du client et leur transformation en une liste d’exigences, la compréhension des critères de dimensionnement tels que spécifiés par la société en fonction des codes de calcul en vigueur, l’élaboration de solutions conceptuelles simples applicables à diverses idées et l’évaluation préliminaire de chacune des idées. Les exigences du projet doivent être aussi claires que possible et inclure des aspects tels que les performances, les paramètres qualitatifs, la fiabilité, la sécurité, la durée de vie du produit, l’esthétique, l’ergonomie, l’économie et l’entretien. Le principal objectif de la recherche systématique est de donner naissance à toute une série de concepts possibles. Le meilleur moyen de faire naître de nouveaux concepts est probablement de combiner la méthode intuitive et la méthode systématique. La recherche systématique permet de développer diverses idées qui sont ensuite appliquées dans le cadre du processus de réflexion intuitif. Le principal objectif de l’évaluation préliminaire est de réduire le nombre de concepts. Cet objectif peut être atteint par l’intermédiaire de discussions ou à l’aide de modèles d’analyse préliminaire. Il est important que la solution proposée soit justifiée et de pouvoir revenir à cette étape à un stade ultérieur du processus. La phase d’analyse inclut le classement des différents concepts, la réalisation d’une analyse simplifiée des risques de chaque concept et la réalisation d’une évaluation finale des concepts. Le classement peut être déterminé en soupesant les objectifs et les exigences afin de pouvoir établir une comparaison systématique entre les différents concepts. Un modèle mettant en rapport le classement des diverses exigences avec les différents concepts est alors produit. Le concept le mieux classé est celui qui occupe la position la plus élevée. L’analyse des risques est un élément majeur de l’étude de conception. Tous les risques éventuels liés aux deux ou trois concepts les mieux classés doivent être listés. Ces risques peuvent concerner la construction, le transport, la production, les intempéries ; il peut s’agir de risques économiques, de risques d’accident, etc. L’objectif du dimensionnement préliminaire (ou prédimensionnement) est d’estimer les dimensions des éléments porteurs d’un bâtiment, tels que les fermes, les poutres, les poteaux, les murs et les planchers. Pour établir les dimensions préliminaires, il convient généralement de déterminer les combinaisons d’actions pertinentes afin d’estimer les forces sectionnelles qui agissent sur la partie structurale analysée. L’estimation des dimensions des sections repose sur :

l’expérience et les recommandations
la valeur de calcul préliminaire des forces (interaction y comprise)
la valeur de calcul préliminaire des contraintes
la valeur de calcul préliminaire de la flèche

2.1.2. Conception détaillée reposant sur une vérification

2.1.2.1. Résultats et processus

Tous les partis architecturaux clés doivent être pris au cours de la phase de conception détaillée. La conception détaillée doit déboucher sur les résultats suivants :

la structure est entièrement et clairement définie et validée
tous les principaux systèmes de construction sont définis
tous les éléments sont entièrement conçus et agencés
les coûts et les méthodes de construction sont établis avec précision
un accord concernant les tolérances est conclu entre les sociétés concernées pour assurer la constructibilité, la préfabrication et le transport
les niveaux de qualité sont définis
des spécifications normatives sont définies en fonction des systèmes prévus et terminés

Le processus de conception structurale est réglementé par le code de conception applicable dans la zone géographique où la structure est destinée à être construite. Dans certains pays, les codes de conception reposent sur des principes tels que le calcul aux états limites, la fiabilité ou la contrainte admissible. Le calcul aux états limites est valable dans la plupart des pays européens et toutes les étapes de ce processus sont décrites dans les différents Eurocodes. Un même code de conception doit être utilisé pour concevoir une structure dans son intégralité.

2.1.2.2. Vérification

La vérification est la partie la plus importante du calcul structural. Depuis 2010, plusieurs codes communs à tous les pays de l’Union européenne, les « Eurocodes », doivent être utilisés pour concevoir des structures. La vérification de la capacité résistante d’une structure ou d’une de ses parties est effectuée à l’état limite ultime, alors que la vérification permettant de savoir si elle fonctionne est réalisée à l’état limite de service. Pour vérifier une structure à l’état limite ultime, le concepteur doit créer des modèles structuraux et de charges en utilisant des valeurs de calculs pour les actions, le matériau ou les propriétés du produit ainsi que des données géométriques. La sélection des cas de charge implique l’identification des combinaisons d’actions, des possibles changements de direction et de position des actions, ainsi que des déformations et imperfections à prendre en compte.

2.2. APPLICATION DES EUROCODES

2.2.1. Les différents Eurocodes et les exigences générales

Les Eurocodes – ensemble de règles techniques harmonisées concernant la conception des structures – ont été établis par la Commission européenne pour remplacer les règles nationales des différents États membres de l’Union européenne. Ils doivent être utilisés conjointement et comprennent les normes suivantes, chacune étant en général constituée d’un certain nombre de parties :

EN 1990 Eurocode 0 : Bases de calcul des structures
EN 1991 Eurocode 1 : Actions sur les structures
EN 1992 Eurocode 2 : Calcul des structures en béton
EN 1993 Eurocode 3 : Calcul des structures en acier
EN 1994 Eurocode 4 : Calcul des structures mixtes acier-béton
EN 1995 Eurocode 5 : Calcul des structures en bois
EN 1996 Eurocode 6 : Calcul des structures en maçonnerie
EN 1997 Eurocode 7 : Calcul géotechnique
EN 1998 Eurocode 8 : Calcul des structures pour leur résistance aux séismes
EN 1999 Eurocode 9 : Calcul des structures en aluminium

Les articles des Eurocodes se caractérisent par deux symboles, utilisés tout au long des textes normatifs. Le premier est la lettre « P » qui signifie « principe ». Les exigences qui suivent cette lettre doivent être respectées. Les principes comprennent des énoncés d’ordre général et des définitions ne comportant pas d’alternative. Lorsque la lettre « P » n’apparaît pas, cela signifie qu’il s’agit d’une « règle d’application » ou une « recommandation ». Ces règles d’application sont des règles généralement reconnues qui sont conformes aux exigences des principes mais elles peuvent être remplacées par d’autres solutions. L’Eurocode 0 définit les principes de calcul aux états limites et des exigences en matière de sécurité, d’aptitude au service et de durabilité des structures. Les exigences générales suivantes concernant le processus de conception sont spécifiées dans l’Eurocode 0 :

le choix du système structural et le projet de structure sont réalisés par un personnel suffisamment qualifié et expérimenté ;
l’exécution est confiée à un personnel suffisamment compétent et expérimenté ;
une surveillance et une maîtrise de la qualité adéquates sont assurées au cours du travail, à savoir dans les bureaux d’études, les usines, les entreprises et sur le chantier ;
les matériaux et produits de construction sont utilisés de la manière spécifiée dans les Eurocodes, ou dans les normes d’exécution appropriées, ou dans les spécifications citées en référence pour les matériaux ou produits ;
la structure bénéficiera de la maintenance adéquate ;
l’utilisation de la structure sera conforme aux hypothèses admises dans le projet.

2.2.2. Situations de projet et vérifications

Pour vérifier une structure ou une de ses parties, le concepteur doit faire une distinction entre les situations de projet (cf. Tableau 2.1), les agents, les actions, les combinaisons d’actions et leurs effets (cf. Figure 2.1). Les agents sont par exemple la gravité, le vent, la neige, le rayonnement solaire, les séismes, etc. Les actions sont par exemple les charges, les pressions, les températures, les accélérations au sol, etc. Les combinaisons d’actions regroupent des actions susceptibles de se produire en même temps. Enfin, les effets sur la structure des combinaisons d’actions peuvent être les contraintes, les forces et les moments internes, les rotations, les déplacements, etc. Les Eurocodes s’appuient sur le calcul aux états limites. L’état limite correspond aux conditions au-delà desquelles la structure ne satisfait plus les exigences de performances requises. Ces conditions sont classées en deux types d’états limites : état limite ultime ou état limite de service. Les états limites ultimes (ELU) concernent la sécurité ; il s’agit des états associés à un effondrement ou à d’autres formes similaires de défaillance structurale. Les états limites de service (ELS) correspondent aux états dans lesquels la structure, bien qu’elle reste debout, se comporte de façon insatisfaisante en raison, par exemple, d’une déformation ou d’une vibration excessive. La Figure 2.1 illustre la méthode de vérification ou de calcul.

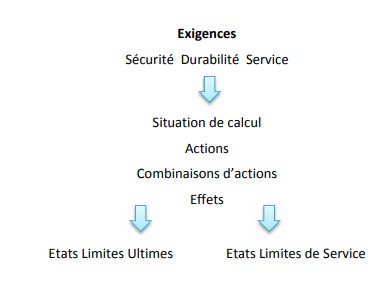
Figure 2.1 : Exigences et terminologie utilisées dans la méthode de calcul.

Tableau 2.1 : situations de projet et vérifications qui leur sont associées.

La conception et les détails des structures en lamellé-collé et en bois doivent être réalisés conformément à l’Eurocode 5. Ce dernier n’est cependant valable qu’en combinaison avec l’Eurocode 0 et l’Eurocode 1, celui-ci concernant tous les types de charge. L’Eurocode 5 se divise en trois parties :

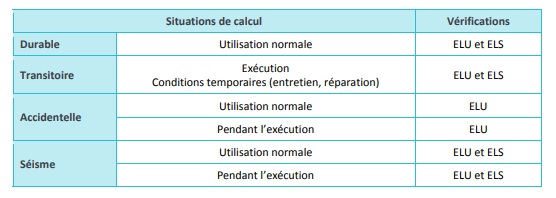
EN 1995-1-1 - Conception et calcul des structures en bois – Partie 1-1 : Généralités – Règles communes et règles pour les bâtiments ;
EN 1995-1-2 - Conception et calcul des structures en bois – Partie 1-2 : Généralités – Calcul des structures au feu ;
EN 1995-2 - Conception et calcul des structures en bois – Partie 2 : Ponts.

Les Eurocodes peuvent contenir des paramètres laissés à choix national (certaines règles de calcul et valeurs de coefficient). Ces paramètres déterminés au niveau national (PDN) sont rassemblés dans l’Annexe Nationale de l’Eurocode en question. À noter que les annexes nationales contiennent également des clauses complémentaires non contradictoires avec les règles Eurocodes.

2.2.3. Principes de calcul aux états limites

L’Eurocode 0 décrit deux méthodes de calcul aux états limites :

méthodes de la fiabilité,
méthode des coefficients partiels.

Le calcul aux états limites repose sur une approche statistique, qui suppose une évaluation de la probabilité d’atteindre un état limite donné, et sur l’établissement du niveau maximum acceptable de cette probabilité à des fins de calcul. Considérons un cas particulier, à savoir lorsque l’état limite de défaillance peut être décrit en termes d’effet de charge E et de résistance R de sorte que la défaillance se produira si E > R (cas fondamental). L’effet de charge E correspond généralement à une valeur maximale pendant une durée de référence T (souvent égale à une année pour les charges variables avec le temps). E et R sont des variables aléatoires. La marge de sécurité définie comme Z = R - E est également une variable aléatoire, de sorte que la structure est considérée comme sûre lorsque Z > 0. Si on part du principe que R et E sont normalement distribués avec des valeurs moyennes µ_R et µ_E, ainsi que des écarts-types σ_R et σ_E, la probabilité de défaillance P_f peut être exprimée par l’équation (2.1).

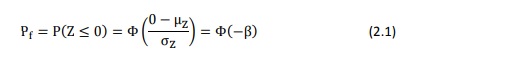
où $phi$ ( ) correspond à la fonction de distribution normale standard, µ_Z = µ_R - µ_E et σ²Z = σ²R + σ²E et β=µ_Z/σZ correspond à l’indice de fiabilité. L’indice de fiabilité β permet de mesurer le niveau de sécurité et de savoir de combien d'écarts-types la zone de défaillance (Z < 0) est éloignée de la valeur moyenne de Z. La relation entre β et P_f est indiquée dans le Tableau 2.2.

Tableau 2.2 : relation entre l’indice de fiabilité et la probabilité de défaillance

Les codes de construction basés sur le calcul aux états limites, tels que l’Eurocode 0, définissent généralement un niveau de sécurité formel en termes d’indice cible minimum de fiabilité β_target(ou probabilité de défaillance maximum admissible). Dans l’Eurocode 0, l’indice cible de fiabilité est fixé à 4,7 pour une durée de référence d’une année et à 3,8 pour une durée de référence de 50 ans. Dans les applications nationales, de nombreux pays autorisent β_target à dépendre des conséquences prévues de la défaillance, définies par les classes de fiabilité. Cela signifie par exemple qu’il est possible d’utiliser des valeurs inférieures pour β_target dans les cas où les conséquences d’une défaillance en termes de vie humaine sont considérées comme faibles et vice versa. Les méthodes de la fiabilité ne sont généralement pas adaptées à un calcul structural ordinaire, mais peuvent être utilisées à des fins de calibration des codes et de comparaison de niveaux de fiabilité des structures. En cas de calcul ordinaire, il est préférable de se servir de la méthode des coefficients partiels.

2.2.4. Vérification basée sur la méthode des coefficients partiels

Dans le cas d’une conception technique normale, l’évaluation basée sur un indice de fiabilité n’est pas pratique. Il est donc préférable d’utiliser la méthode des coefficients partiels de sécurité. Cette méthode utilise plusieurs coefficients de sécurité (coefficients partiels), chacun d’entre eux prenant en compte les divers types d’incertitude ayant une incidence sur les calculs. Par exemple :

incertitude dans les valeurs représentatives des actions (γ_f)
incertitude dans les propriétés des matériaux (γ_m)
conséquences d’une défaillance (γ_d)

Le concept de valeur caractéristique, qui doit reposer sur une définition statistique claire, constitue la base de la méthode des coefficients partiels de sécurité. Les actions caractéristiques (communément appelées « charges ») sont définies dans l’Eurocode 1. Les valeurs de calcul des actions sont obtenues en multipliant les actions caractéristiques . La valeur d'un coefficient partiel de sécurité pour γ par les coefficients partiels de sécurité les charges et les propriétés des matériaux dépend de la définition de la valeur caractéristique utilisée. Dans le cas des actions variables avec le temps (telles que la neige et le vent), une définition typique de la valeur caractéristique Q_k est que la probabilité de dépasser Q_k doit être de 2 % par an. Cela revient à dire que Q_k doit avoir une période de retour de 50 ans, ce qui signifie que sur une période de 50 ans, le niveau de charge Q_k n’est dépassé qu’une seule fois en moyenne. Concernant le cas fondamental à l’état limite ultime, il convient de vérifier que la résistance de calcul R_d est supérieure à l’effet de charge de calcul E_d pour l’élément structural considéré.

Cette exigence doit être vérifiée pour chaque mode de défaillance et un certain nombre de combinaisons d’actions différentes selon la situation de projet. La valeur de calcul E_d de l’effet de charge est déterminée sur la base des actions permanentes G, des actions variables avec le temps Q et des actions accidentelles. La valeur de calcul G_d des actions permanentes est déterminée par :

où γ_G correspond à un coefficient partiel de sécurité pour la charge permanente G et G_k à la valeur caractéristique des actions permanentes, habituellement définie comme le fractile à 50 % ou la valeur moyenne.
Les valeurs de calcul des actions variables sont définies par :

où γ_Q correspond à un coefficient partiel de sécurité pour l’action variable Q et Q_k à la valeur caractéristique de l’action variable Q, habituellement définie comme le fractile à 98 % de la distribution pour les maximums annuels de Q.
La valeur de calcul R_d de la résistance est principalement déterminée sur la base des propriétés des matériaux et des dimensions. La valeur de calcul f_d du paramètre de résistance f est définie par :

où γ_M correspond au coefficient partiel de sécurité associé au matériau, f_k à la valeur caractéristique des propriétés du matériau, habituellement définie comme le fractile à 5 %, et η à un coefficient représentant les différences entre les conditions in situ applicables à la structure et les conditions d’essais utilisées pour déterminer les propriétés.

À l’état limite de service, la condition critique est généralement formulée de telle sorte que la valeur de calcul de la flèche, de la vibration, du glissement dans un assemblage, etc. doit être inférieure à une valeur requise absolue ou relative.

L’application de la méthode des coefficients partiels peut varier d’un pays à l’autre.

2.2.5. Effets de charge et combinaisons d’actions

L’expression « effets de charge » couvre par exemple les moments ou les forces internes ainsi que les flèches induites par les charges. En principe, la structure n’est pas conçue pour une charge unique, mais pour une combinaison d’actions (poids propre et charge de neige, par exemple). Pour obtenir une valeur de combinaison de calcul pour chaque situation de charge, chaque action doit être considérée à tour de rôle comme une action dominante (valeur totale) et être combinée aux autres actions considérées avec leurs valeurs de combinaison, définies par une réduction de la valeur caractéristique Q_k par les coefficients ψ₀, ψ₁ et ψ₂ comme suit :

La valeur de combinaison (ψ₀Q_k), utilisée pour la vérification d’ELU et pour les combinaisons caractéristiques d’ELS irréversibles (ELS pour lesquels certaines conséquences d’actions entraînant un dépassement des exigences de service spécifiées subsisteront lorsque les actions auront disparu).
La valeur fréquente (ψ₁Q_k), utilisée pour la vérification d’ELU impliquant des actions accidentelles et pour la vérification d’ELS réversibles. La valeur fréquente est choisie telle que le temps de dépassement corresponde à 1 % de la durée.
La valeur quasi-permanente (ψ₂Q_k), utilisée pour l’évaluation des effets à long terme d’un ELS, tels que les flèches ou les fissures, et pour la représentation d’une action variable dans les combinaisons accidentelles d’un ELS. Correspond à la moyenne temporelle de l’action variable Q.

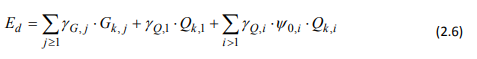
où les indices j et i désignent respectivement la j ième composante d’action permanente et la i ième composante d’action variable, et

Q_k,1 correspond à la valeur caractéristique de l’action variable dominante
γ_Q,1 correspond au coefficient partiel de sécurité associé à Q_k,1

L’annexe nationale française de l’Eurocode 0 indique qu’il n’est en général pas nécessaire de considérer plus de deux actions variables agissant simultanément.

2.2.6. Classes de sécurité

Le risque que la défaillance d’une structure provoque des lésions corporelles graves dépend du type de bâtiment (classé selon son utilisation) et des parties du bâtiment concernées (classées selon leur fonction). Le risque de lésion corporelle est par exemple plus élevé en cas de défaillance d’une poutre de toiture qu’en cas de défaillance d’un montant dans une cloison. Il sera également plus élevé si la poutre soutient la toiture d’une salle de sport que s’il s’agit d’un porche.

Certains pays tiennent compte de ces différences en rattachant les structures porteuses à différentes classes de sécurité en fonction des conséquences d’une défaillance structurale. La classe de sécurité détermine l’importance du contrôle ou la valeur du coefficient partiel γ_d à l’état limite ultime. Lorsque la classe de sécurité est incluse dans le format général de l’équation 2.6, elle influence la valeur de calcul totale de l’effet de charge Ed (cf. Éq. 2.7). Il existe trois classes de sécurité différentes : la classe de sécurité 1 (γ_d = 0,83), qui suppose un faible risque de lésions corporelles graves ; la classe de sécurité 2 (γ_d = 0,91), qui suppose un risque moyen de lésions corporelles graves ; et la classe de sécurité 3 (γ_d = 1) qui suppose un risque élevé de lésions corporelles graves. À l’état limite de service cependant, aucune distinction n’est faite entre les classes de sécurité. Les Eurocodes ne mentionnent actuellement aucun rattachement à des classes de sécurité.

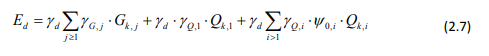
2.3. CONCEPTS UTILISES POUR LE CALCUL AUX ETATS LIMITES DU LAMELLECOLLE ET DU BOIS

En tant que matériaux de construction, le lamellé-collé et le bois se différencient de l’acier, du béton armé ou d’autres composites par diverses caractéristiques. Le bois est une matière biologique et naturelle qui possède des propriétés extrêmement variables. Il s’agit d’un matériau orthotrope, c’est-à-dire que ses propriétés varient selon les directions, et hygroscopique, ce qui signifie que sa teneur en humidité varie en fonction de l’humidité relative de l’air ambiant. Certaines caractéristiques sont propres à la conception de structures en bois lamellé collé :

la teneur en humidité du bois et les classes de service ;
la durée de charge pour différents types de charge ;
les coefficients partiels pour les propriétés des matériaux et les ajustements à l’aide
de divers coefficients de modification ;
l’augmentation possible des valeurs de calcul de la flexion et de la traction en raison
de l’effet d’échelle ;
les différentes réponses du matériau lorsque les charges sont appliquées dans
différentes directions en lien avec l’orientation du fil du bois.

2.3.1. Effet de la teneur en humidité et classes de service

La teneur en humidité et les variations de la teneur en humidité ont une incidence élevée sur toutes les propriétés des produits à base de bois et notamment du lamellé-collé. La teneur en humidité affecte à la fois la résistance et la rigidité. Pour tenir compte de cet effet lors de la conception, trois classes de services ont été définies dans l’Eurocode 5, à savoir :

La classe de service 1, qui se caractérise par une humidité dans les matériaux correspondant à une température de 20 °C et une humidité relative de l’air environnant ne dépassant 65 % que quelques semaines par an. L’humidité moyenne dans la plupart des bois résineux n’excède pas 12 %. Cette classe inclut, par exemple :
o les éléments dans les de bâtiments chauffés en permanence ;
o les planchers au-dessus de vides sanitaires aérés par de l’air intérieur ;
o Les structures en bois lamellé collé qui couvrent des piscines intérieures dont l’ambiance est correctement contrôlées pour permettre d’atteindre les conditions de cette classe.
La classe de service 2, qui se caractérise par une humidité dans les matériaux correspondant à une température de 20 °C et une humidité relative de l’air environnant ne dépassant 85 % que quelques semaines par an. L’humidité moyenne dans la plupart des bois résineux n’excède pas 20 %. Cette classe inclut, par exemple :
o les planchers et les fermes de greniers non chauffés, mais aérés ;
o les planchers au-dessus de vides sanitaires aérés par de l’air extérieur ;
o les structures en bois lamellé-collé dans des pièces ou des bâtiments qui ne sont pas chauffés en permanence, comme les maisons secondaires, les locaux de stockage non chauffés, les manèges non isolés et les bâtiments agricoles ;
o les structures en bois lamellé-collé qui couvrent les piscines mal aérées.
La classe de service 3, qui se caractérise par des conditions climatiques amenant des humidités supérieures à celles de la classe de service 2. L’humidité moyenne dans la plupart des bois résineux excède 20 %. Cette classe inclut, par exemple :
o les structures en bois lamellé-collé dans des pièces ou des bâtiments où l’humidité est occasionnée par des processus ou un stockage ;
o les structures qui ne sont pas protégées de l’humidité ou qui sont en
contact direct avec l’eau.

2.3.2. Classes de durée de charge

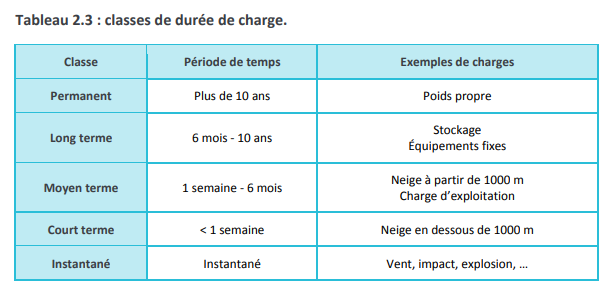
Le bois subit une importante perte de résistance sur une période de temps donnée. Des classes de durée de charge ont été établies pour tenir compte de cette perte de résistance et faciliter le calcul. Les classes de durée couvrent toute une série de durées pouvant s’appliquer dans la pratique et les actions qui leur sont associées (cf. Tableau 2.3).
L’influence de la durée de charge sur la capacité résistante du bois lamellé-collé est prise en compte en attribuant un coefficient k_mod en fonction de la classe de service et de l’une des cinq classes de durée de charge présentées dans le Tableau 2.3. Le coefficient de durée de charge kmod est un coefficient de réduction pour la résistance caractéristique du bois, du lamellé-collé et des autres produits à base de bois qui varie entre 0,2 et 1,1. Ce coefficient est de 1,1 et engendre une augmentation de la résistance caractéristique seulement en cas de charge instantanée et de lamellé-collé sec (classes de service 1 et 2 conformément à la norme EN 14080).

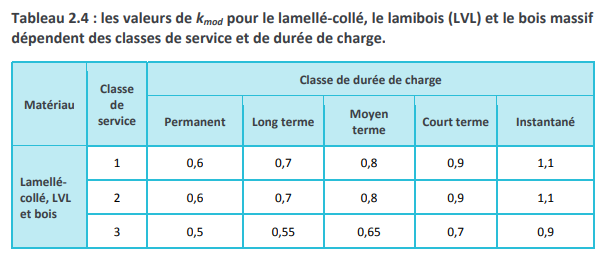
Les valeurs du coefficient de modification k_mod sont indiquées dans le Tableau 2.4. Si la combinaison d’actions consiste en des actions appartenant à différentes classes de durée de charge, il convient d’utiliser pour kmod une valeur qui correspond à l’action ayant la plus courte durée d’application.

Lorsqu’un assemblage est constitué de plusieurs éléments en bois ayant différentes valeurs de k_mod, le coefficient de modification de résistance peut être déterminé par :

où k_mod,i correspond au coefficient de modification de résistance des éléments 1 et 2.

2.3.3. Calcul aux états limites ultimes des éléments en bois lamellé-collé

La valeur de calcul de la capacité résistante à l’état limite ultime est déterminée sur la base de la valeur de calcul de la résistance du bois lamellé-collé. Tout d’abord, la valeur caractéristique f_k est prise à partir de l’un des Tableaux 1.1 – 1.3, qui donnent les propriétés de résistance et de rigidité caractéristiques courantes en N/mm² et les masses volumiques en kg/m^3. Ensuite, la valeur de calcul f_d pour la propriété adéquate est calculée conformément à l’équation 2.5. Pour le bois lamellé-collé, l’équation 2.9 s’applique.

La valeur caractéristique f_k est ajustée en utilisant k_mod suivant le type de charge et la classe de service et selon le coefficient partiel γ_M qui est de 1,25 pour le bois lamellé-collé en raison des incertitudes qui lui sont associées. Les classes de résistance du lamellé-collé étant certifiées et le processus de fabrication du lamellé-collé étant soumis à un contrôle spécifique, la valeur du coefficient partiel γ_M est inférieure à celle applicable pour le bois massif.

Dans le cas des sections transversales rectangulaires dont la hauteur est inférieure à 600mm, les valeurs caractéristiques de la résistance à la flexion f_m,k et de la résistance caractéristique à la traction parallèle au fil f_t0,k peuvent être augmentées du coefficient k_h (coefficient d’effet d’échelle). Pour les autres propriétés de résistance caractéristique, le coefficient k_h est égal à 1.

où h correspond à la hauteur (en mm) de la section transversale.
Conformément aux règles définies dans l’Eurocode 5, la résistance à la flexion et à la traction doit être corrigée en fonction des effets d’échelle. Dans les règles actuelles, la capacité en cisaillement du bois lamellé-collé est réduite du coefficient k_cr.

2.3.4. Calcul aux états limites de service des éléments en bois lamellé collé

À l’état limite de service, la structure doit être suffisamment rigide pour éliminer toute vibration ou déformation susceptible de perturber les fonctions d’un élément du bâtiment (évacuation des eaux du toit, par exemple). La rigidité d’un élément lamellécollé est affectée par sa géométrie ainsi que par plusieurs facteurs. Ces facteurs sont la durée de la charge, la teneur en humidité et la température du matériau. Les variations de charge et la teneur en humidité (qui inclut les changements d’humidité) sont particulièrement importantes.

Au moment de calculer la déformation, il convient de définir les charges à prendre en compte. Trois combinaisons d’actions différentes peuvent être appliquées afin de définir les situations de projet voulues. Les combinaisons d’actions pour les états limites de service sont définies dans l’Eurocode 0. De plus amples informations sur le calcul de la déformation initiale et finale des éléments lamellés collés et des pièces d’assemblage sont fournies dans le chapitre 6.

2.4. RECOMMANDATIONS RELATIVES AUX CONTRE-FLECHES ET LIMITE DES FLECHES

D’un point de vue esthétique, il est préférable de limiter la flèche des poutres de toiture, par exemple. Même lorsqu’elles n’excèdent pas 1/300 de la portée, les flèches sont visibles, en particulier en cas de lignes de référence horizontales. Les exigences visuelles varient cependant en fonction du type de bâtiment – elles sont par exemple moins élevées pour un local de stockage que pour un hall d’exposition.

2.4.1. Contre-flèche

Il est possible de remédier, dans une certaine mesure, aux inconvénients des flèches en prévoyant un certain nombre de contre-flèches dans la structure. L’ampleur de la contreflèche peut correspondre à la flèche induite par le poids propre calculé (plus éventuellement la valeur normale de la charge variable). Ceci confère normalement une horizontalité lors de l’utilisation. La contre-flèche est avant tout pertinente dans le cas des poutres sur appuis libres dont la portée atteint 6 à 8 m. Les poutres continues qui reposent sur plusieurs appuis n’ont, en principe, pas besoin de contre-flèches.
La contre-flèche doit toujours être spécifiée lorsque la pente d’une toiture est modérée.
Elle doit être conçue de sorte que la pente mène vers les gouttières, même en cas de pleine charge de neige. Si tel n’est pas le cas, l’eau stagnante provenant de la neige fondue, de la neige et de la glace peut entraîner une augmentation de la flèche et, de ce fait, un risque de rupture au niveau des poutres de toiture. En outre, le risque de fuite et de dégâts des eaux est élevé. Une pente de 3% minimum doit toujours être visée.

2.4.2. Flèches

Le chapitre 6 présente les flèches acceptables pour les éléments droits par rapport à la portée de plusieurs types d’éléments. Ces informations peuvent également être utilisées pour les arcs, les portiques et d’autres structures.
L’assemblage à des murs intérieurs non porteurs doit être conçu de façon à ce que le plancher puisse fléchir librement sans transférer les charges au mur. Si tel n’est pas le cas, le mur risque d’être endommagé et/ou de surcharger le plancher en dessous. Les exigences concernant la limite des flèches sont généralement moins élevées pour les structures secondaires que pour la structure principale. Cependant, cela ne doit pas entraîner une altération des fonctions (rupture des matériaux de couverture, par exemple).