4.1. POUTRES
Les poutres sont généralement des éléments lamellés collés droits de section rectangulaire qui travaillent en flexion. Elles peuvent être utilisées pour les ponts, les solives de plancher, les poutres de toiture, les pannes, etc. Les poutres à inertie variable et les poutres courbes sont présentées dans les chapitres 7 et 11.
Dans le cas des poutres, il convient de procéder à des vérifications concernant la résistance mécanique (en général la flexion et le cisaillement), les flèches et les vibrations. La compression perpendiculaire au fil doit également être vérifiée au niveau des appuis des poutres. Différents critères de dimensionnement peuvent s’avérer déterminants selon la longueur de la poutre. Pour les poutres de portée moyenne, la flexion est très importante, alors que dans le cas des poutres de portée courte à moyenne fortement sollicitées, c’est le cisaillement qui est crucial. Dans le cas des poutres à longue portée, les critères d’aptitude au service en matière de déformations et de vibrations peuvent également être déterminants. Dans le cas des poutres de portée L moyenne et en appui simple soumises à une charge uniformément répartie, les hauteurs de poutre correspondent environ à L/20 pour le moment de flexion et à L/30 pour le cisaillement (selon la sollicitation).
4.1.1. Flexion et cisaillement
Selon la théorie de la flexion élastique, lorsqu’un élément rectangulaire plein est soumis à un moment de flexion M selon l’axe fort (y-y), la contrainte normale à n’importe quelle distance z de la fibre neutre est définie par :

où Iy correspond au moment d’inertie de la section transversale de l’élément selon l’axe y-y. Pour calculer les contraintes maximales au niveau des bords supérieur et inférieur d’une poutre de section rectangulaire, le module d’inertie Wy selon l’axe fort est utilisé :

b correspondant à la largeur de la poutre et h à sa hauteur. Il est ensuite possible de calculer la contrainte de flexion maximale dans la section transversale en divisant le moment de flexion de calcul M de la poutre lamellée collée par le module d’inertie :

Il est possible de déduire des expressions similaires concernant la flexion selon l’axe faible de l’élément. Si un élément travaille en flexion selon deux axes (fort et faible) en même temps, les conditions de calcul à satisfaire sont données par :

où σm,y,d et σm,z,d sont les valeurs de calcul des contraintes de flexion selon les axes principaux et fm,y,d et fm,z,d les valeurs de calcul correspondantes pour les résistances à la flexion. À noter que pour le bois lamellé collé, la résistance à la flexion sur l’axe faible n’est pas la même que la résistance à la flexion sur l’axe fort en raison de l’effet système et des différentes qualités des lamelles. Le coefficient de modification km traduit la possibilité de redistribution des contraintes ainsi que l’inhomogénéité du matériau. Pour les éléments lamellés collés de section rectangulaire, km = 0,7. Pour les autres sections, km = 1,0.
Tous les éléments qui travaillent en flexion sont également soumis à des contraintes de cisaillement parallèles à l’axe de la poutre. Dans une poutre, les contraintes de cisaillement maximales interviennent au niveau de l’axe neutre et sont égales à zéro aux bords. Dans le cas des sections rectangulaires, la contrainte de cisaillement maximale τ (au niveau de l’axe neutre) est donnée par :

où V correspond à l’effort tranchant, b à la largeur de la poutre et h à la hauteur de la poutre. Dans le cadre du calcul, il convient de satisfaire l’expression suivante :

où τd correspond à la valeur de calcul de la contrainte de cisaillement et fv,d à la valeur de calcul de la résistance au cisaillement. En raison de la fissuration du bois due à des contraintes induites par l’humidité, l’Eurocode 5 recommande de ne pas utiliser la largeur totale b de l’élément lamellé collé, mais une largeur efficace bef = kcr·b, avec bef < b. Les différentes valeurs de kcr en fonction, principalement, du type de bois sont indiquées dans les documents d’application nationale de l’Eurocode 5. En France, le coefficient kcr dépend des conditions d’exposition (classes de service) ; les valeurs sont données dans le tableau ci-dessous.
Tableau 4.1 : Valeurs du coefficient de fissuration kcr selon les classes de service

4.1.2. Traction et traction/flexion combinées
Les éléments lamellés collés droits peuvent être soumis à des efforts axiaux (traction ou compression) ou à des efforts axiaux combinés à une flexion. Lorsqu’un élément est sollicité en traction, il convient de prendre en compte son volume, car la résistance dépend du volume (maillon le plus faible de Weibull). Lorsqu’ils sont sollicités en compression, les éléments courts subissent une rupture en compression alors que les éléments élancés subissent une rupture par flambement.
Dans le cas d’éléments droits soumis à une force de traction axiale et/ou à une flexion, le critère de dimensionnement suivant s’applique :

où σt,0,d correspond à la valeur de calcul de la contrainte de traction parallèle au fil, σm,y,d et σm,z,d aux valeurs de calcul des contraintes de flexion selon les axes principaux. ft,0,d correspond à la valeur de calcul de la résistance à la traction, et fm,y,d et fm,z,d aux valeurs de calcul des résistances à la flexion. km correspond à un coefficient de modification (sections rectangulaires : km = 0,7, autres sections : km = 1,0).
4.1.3. Déversements
Les éléments droits élancés sont soumis au déversement si rien n’empêche le bord comprimé de l’élément de se déplacer hors du plan. Le déversement intervient alors à des contraintes inférieures à la résistance à la flexion.
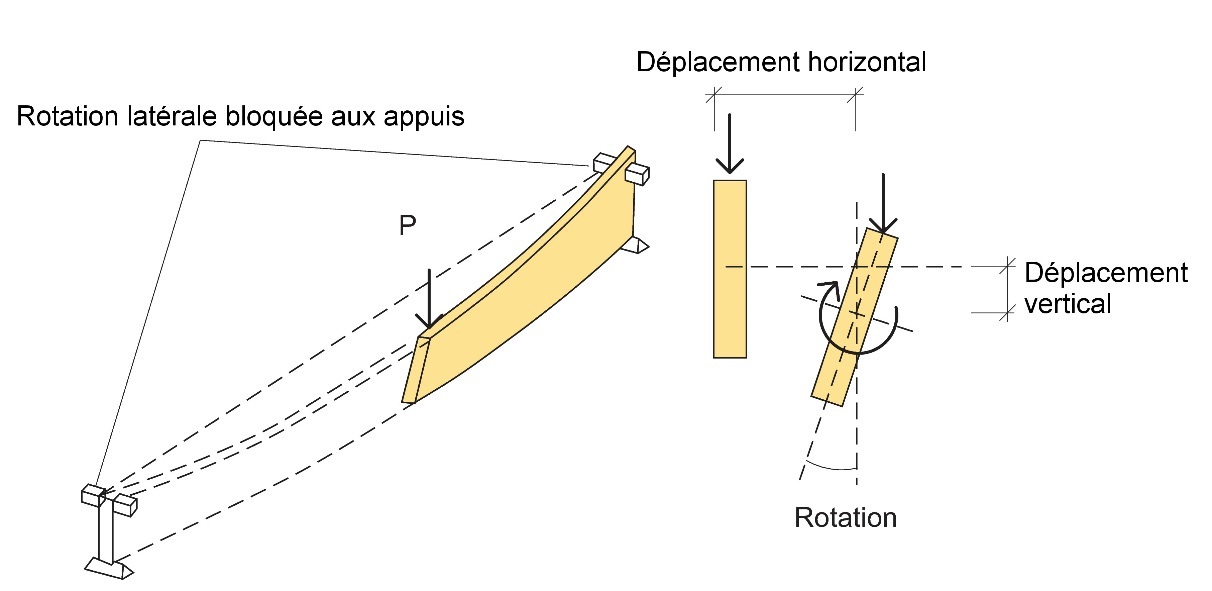
Figure 4.1 : Déversement d’une poutre en appui simple
En réalité, il est rare que les éléments élancés soient complètement droits, ce qui accroît le risque de déplacement hors-plan. D’autres paramètres influencent le risque de déversement : les conditions d’appui (libre, articulé ou encastré), le type de sollicitation, l’emplacement de la sollicitation (bord/axe neutre), le type d’anti-dévers et la distance entre chaque anti-dévers. Ces facteurs affectent la longueur efficace lef, utilisée dans les équations de dimensionnement.
La contrainte de flexion critique σm,crit à laquelle le déversement d’une poutre lamellée collée de section rectangulaire pleine intervient peut être formulée comme suit :

où b et h correspondent respectivement à la largeur et à la hauteur de la poutre, lef à la longueur efficace compte tenu du type de sollicitation (répartition des moments de flexion), d’appuis et d’anti-dévers, et E0,05 à la valeur caractéristique à 5 % d’exclusion du module d’élasticité dans le sens du fil. Dans le cas d’une poutre en appui simple soumise à une charge de moment uniformément répartie et à une charge appliquée au niveau de l’axe neutre de la poutre, lef peut être remplacé par la portée de la poutre l. Les rapports entre lef et l dans différentes conditions sont indiqués dans le Tableau 4.2. Ces rapports sont valables pour les poutres dont les appuis sont limités et sollicitées en leur centre de gravité. Si la charge est appliquée sur le bord comprimé de la poutre, lef doit être augmenté de 2.h ; si elle est appliquée sur le bord tendu de la poutre, lef peut être diminué de 0,5.h. Les poutres contreventées au niveau du bord comprimé à intervalles a à l’aide de contreventements suffisamment rigides ont une longueur efficace de lef = a.
Tableau 4.2 : longueur efficace en fonction de la portée de la poutre. Poutre sollicitée en son centre de gravité. Si la charge est appliquée sur le bord comprimé de la poutre, lef doit être augmenté de 2h ; si elle est appliquée sur le bord tendu de la poutre, lef doit être diminué de 0,5h.

Le rapport relatif d’élancement en flexion λrel,m peut être calculé à partir de la valeur caractéristique de la résistance à la flexion fm,k et de la contrainte de flexion critique σm,crit :

Lorsque le rapport d’élancement λrel,m < 0,75, les poutres sont stables et ne sont pas soumises à une instabilité latérale. Lorsque λrel,m > 1,4, le mode de rupture correspond au déversement. Lorsque les rapports d’élancement se situent entre ces valeurs, la rupture intervient en flexion suite à des déformations importantes dans les directions verticale et latérale. Le coefficient kcrit, qui tient compte du déversement, est présenté dans le Tableau 4.3 et la Figure 4.2 en fonction du rapport d’élancement.
Les contraintes de flambement critiques d’éléments autres que des poutres droites (arcs et poutres à section variable, par exemple) sont mentionnées dans les Chapitres 7 et 11.
Tableau 4.3 : valeurs de kcrit en fonction de λrel,m
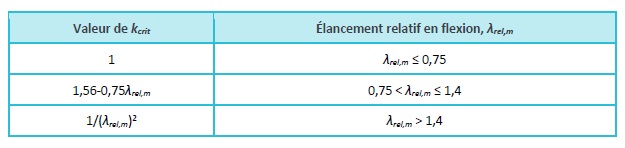
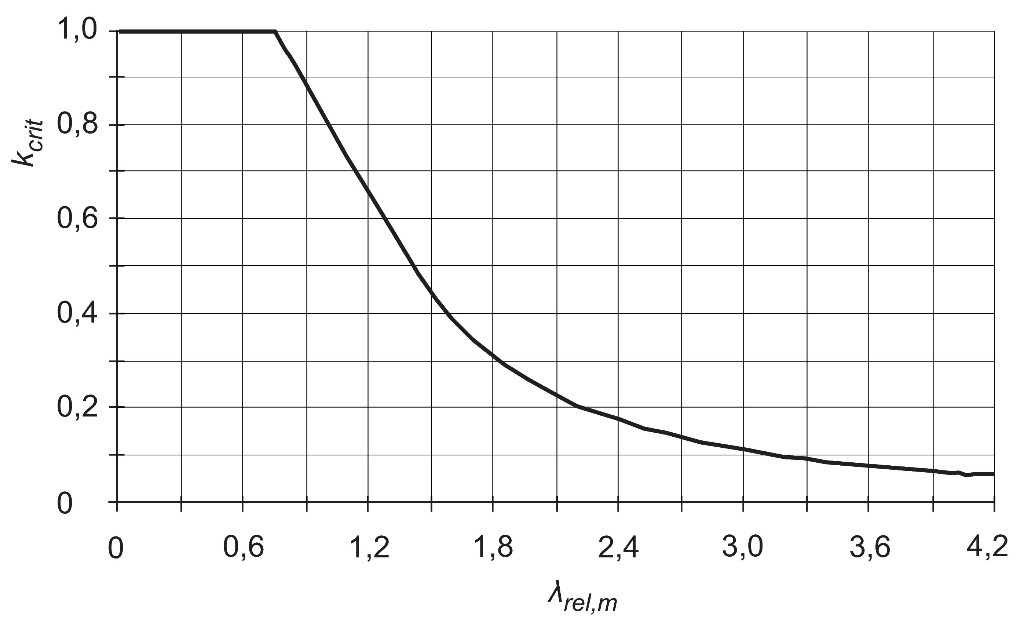
Figure 4.2 : Valeurs de kcrit en fonction de λrel,m ; représentation graphique.
Dans le cas des éléments qui travaillent seulement en flexion selon l’axe fort, les contraintes doivent satisfaire l’expression suivante :

où σm,d correspond à la valeur de calcul de la contrainte de flexion, fm,d à la valeur de calcul de la résistance à la flexion et kcrit au coefficient de modification qui tient compte du déversement.
Les éléments sollicités par une combinaison de flexion et de force de compression axiale et ceux soumis à une compression perpendiculaire au fil sont abordés plus loin.
Le contreventement des poutres élancées doit être disposé en continu ou à intervalles déterminés le long du bord comprimé (cf. Figure 4.3). Il est possible d’obtenir un contreventement continu en fixant une plaque ou un panneau de toiture au bord supérieur d’une poutre en appui simple. Un contreventement à intervalles déterminés peut être réalisé à l’aide de pannes fixées au bord comprimé de la poutre. Dans le cas des poutres continues, le contreventement doit se situer au niveau des appuis intermédiaires sur le bord inférieur (cf. Figure 4.4). Le contreventement peut par exemple être réalisé à l’aide de câbles allant du toit au bord inférieur de la poutre, auquel cas il ne supporte aucune force de compression. Autrement, la sollicitation asymétrique du toit et la flèche du toit qui en découle peuvent amener la poutre à être poussée sur le côté au niveau du bord inférieur. Lorsqu’une poutre élancée est contreventée contre le flambement latéral, le concepteur doit toujours tenir compte de la rigidité du contreventement latéral et du contreventement du système dans son intégralité, et non pas seulement de la poutre. La Figure 4.5 présente différentes longueurs de flambement en fonction du type de contreventement du système considéré dans son intégralité. En cas de doute, il est préférable de supposer l’absence d’un quelconque contreventement latéral ou de l’évaluer en tant que maintien élastique. Le contreventement latéral est très important. De nombreuses ruptures sont intervenues par le passé en raison d’un contreventement latéral inadéquat pendant la phase de montage (c’est-à-dire avant la mise en place du contreventement) ou une fois la structure terminée. Un contreventement trop rigide peut provoquer un effondrement en cascade (lorsqu’une poutre de toiture s’effondre, elle entraîne d’autres poutres de toiture), alors qu’il contribue à la solidité des structures lorsque sa rigidité est adéquate. Le contreventement et sa rigidité sont traités de façon plus approfondie dans le Chapitre 13.
Figure 4.3 : Contreventement latéral de poutres élancées.
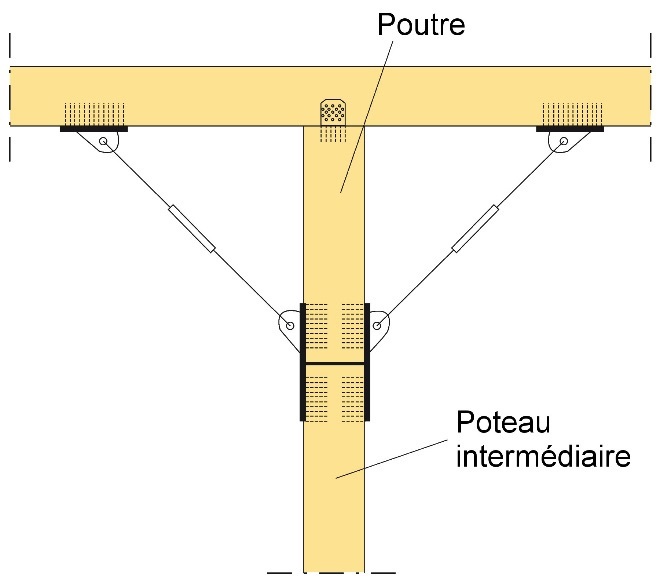
Figure 4.4 : Contreventement latéral d’une poutre élancée au niveau du bord inférieur – au-dessus d’un appui intermédiaire – reliée à la charpente de comble. Ce contreventement ne doit pas supporter de forces de compression. En cas de sollicitation asymétrique du toit induisant une flèche du toit sur un des côtés de la poutre, et si le contreventement peut supporter des forces de compression, le contreventement risque de pousser la poutre et de provoquer un flambement latéral.
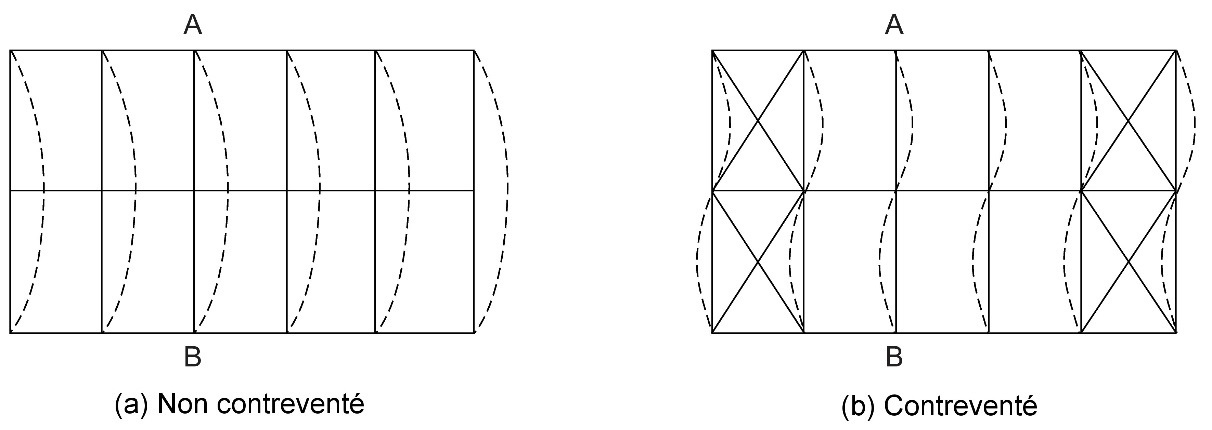
Figure 4.5 : Flambement latéral d’une toiture ou d’une structure de plancher.
4.1.4. Compression perpendiculaire au fil
Dans de nombreuses applications structurales (appuis de poutres et bâtiments à plusieurs étages, par exemple), les éléments en bois sont sollicités perpendiculairement au sens du fil. Le bois se caractérise par une faible rigidité perpendiculaire au fil et par des jeux liés à l’humidité (retrait et gonflement) dans ce sens, ce qui provoque des déformations importantes. Ceci est particulièrement problématique dans le cas des bâtiments à plusieurs étages où les déformations de divers étages s’additionnent. Il est possible de distinguer différents types de ruptures en fonction de la configuration (sollicitation, appuis) (cf. Figure 4.6). Cette figure montre qu’en principe la charge n’est pas seulement transférée par l’intermédiaire de la surface de contact réelle, mais aussi par une surface de contact efficace, élargie par les zones de bois voisines non soumises à une contrainte.
Les déformations dues à une compression perpendiculaire au fil ne provoquent pas de rupture ultime, mais posent un problème en ce qui concerne l’état limite de service. Dans les codes, cependant, ce problème est considéré comme étant lié à l’état limite ultime. L’approche de calcul consiste donc à vérifier les contraintes existantes vis-à-vis de la résistance perpendiculaire au fil plutôt que d’utiliser les valeurs de rigidité. En outre, les réductions de résistance liées à la classe de service (humidité) et au type de charge (durée de charge) sont prises en compte pour calculer la valeur de calcul de la résistance (coefficient de modification kmod) (cf. Sections 2.3.1 et 2.3.2, Éq. 2.9 et Éq. 4.12). (Pour la résistance perpendiculaire au fil, aucun effet d’échelle n’étant pris en compte, le coefficient kh = 1) Par ailleurs, la rigidité perpendiculaire au fil est relativement constante par rapport aux plages d’humidité observées dans les bâtiments (teneur en humidité comprise entre 10 et 20 %) et la résistance à la compression ne varie que très peu dans cette plage d’humidité. Ceci n’étant cependant pas reflété dans le calcul, de très grandes surfaces de contact sont nécessaires pour satisfaire les équations de dimensionnement. Or les grandes surfaces de contact entraînent une déformation non uniforme et sont donc susceptibles de générer des charges décentrées dont ne tiennent pas compte les calculs (Figure 4.7).
NOTE : Un moyen de résoudre ce problème consiste à utiliser la valeur caractéristique de la résistance à la compression perpendiculaire au fil plutôt que la valeur de calcul de la résistance correspondante dans l’équation de dimensionnement (Éq. 4-11). Cela signifie en d’autres termes que les coefficients kmod et γm doivent tous deux être définis comme étant égaux à 1,0. Cette méthode, non normative, ne vaut cependant que pour les structures en bois qui se caractérisent par des rapports relativement faibles entre le poids propre et la surcharge (gk/qk ≤ 0,4 par exemple). Dans le cas d’une structure en bois ordinaire (gk/qk ≤ 0,4, durée de charge moyenne et classe de service 1 ou 2), la méthode entraîne une réduction de la surface de contact nécessaire de 36 % (kmod/γm = 0,8/1,25 = 0,64) par rapport à la surface de contact qui serait nécessaire si la valeur de calcul de la résistance était utilisée. Lorsqu’une structure en bois est soumise à des charges permanentes plus lourdes (gk/qk >0,4) cependant, il convient d’utiliser la valeur de calcul de la résistance à la compression perpendiculaire au fil.
Dans de nombreuses applications, les assemblages entre les poutres et les poteaux sont désormais renforcés. Le renforcement peut notamment prendre la forme de goujons collés en acier ou en bois, de vis autotaraudeuses ou de plaques perforées externes (cf. Figure 4.8). L’avantage d’un assemblage renforcé comparé à un assemblage non renforcé est qu’il réduit le risque de déformation et accroît donc la capacité portante. Dans le cas des vis autotaraudeuses, le mode de rupture peut intervenir de différentes manières : enfoncement des vis dans le bois, flambement des vis et rupture due au fait que la résistance à la compression perpendiculaire au fil du bois est atteinte dans un plan formé par l’extrémité des vis. L’Eurocode 5 ne fournit aucune équation de dimensionnement pour les éléments renforcés soumis à une compression perpendiculaire au fil. Il existe cependant des modèles de calcul qui décrivent la capacité d’un élément renforcé comme étant la somme de la capacité du bois et de la capacité de l’élément de renforcement. Pour calculer la capacité de l’élément de renforcement, il convient de prendre en compte tous les éventuels modes de ruptures ; les différents modes de ruptures dépendent de la géométrie de la poutre et du nombre d’éléments de renforcement. Dans le cas d’appuis de poutre renforcés à l’aide de quelques vis courtes, la capacité résistante des appuis de poutre renforcés se caractérise par l’enfoncement des vis dans le bois. La résistance à la compression perpendiculaire au fil est simultanément atteinte au niveau de la surface de contact. Dans le cas des vis, la résistance à l’enfoncement est considérée comme étant égale à la résistance à l’arrachement. Lorsque les appuis de poutre sont renforcés à l’aide de vis élancées, celles-ci subissent un flambement. Comme dans le premier cas, la résistance à la compression perpendiculaire au fil est simultanément atteinte au niveau de la surface de contact. Dans le cas des appuis de poutre renforcés à l’aide de nombreuses vis courtes, la capacité résistante se caractérise par l’atteinte de la résistance à la compression perpendiculaire au fil du bois dans un plan formé par l’extrémité des vis.
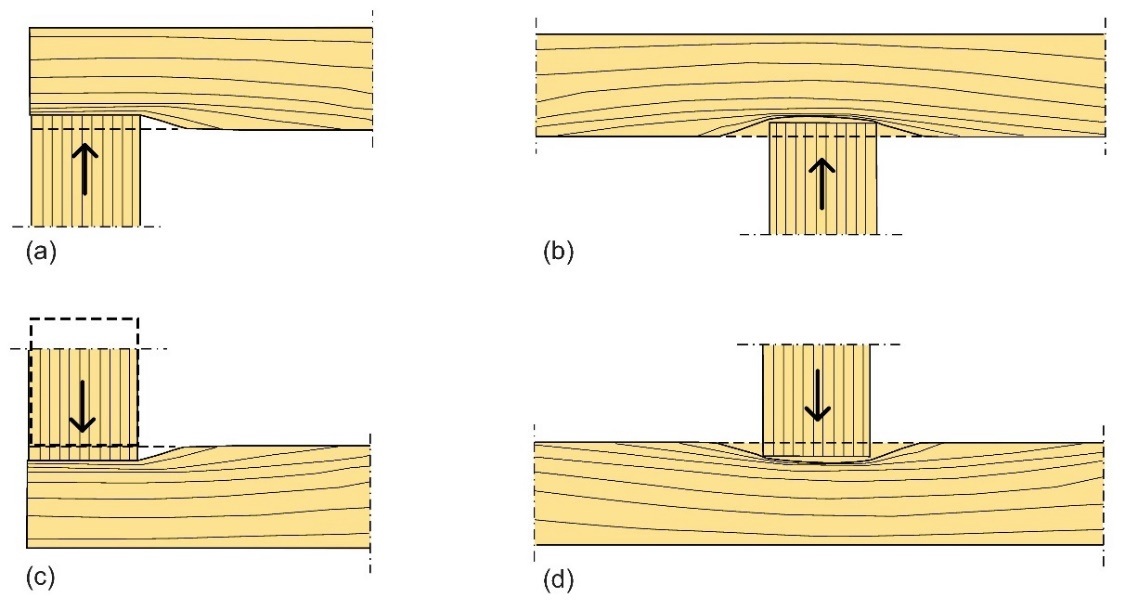
Figure 4.6 : Rupture en compression perpendiculaire au fil. (a) et (b) : éléments sur appuis discrets ; (c) et (d) : éléments sur appui continu.
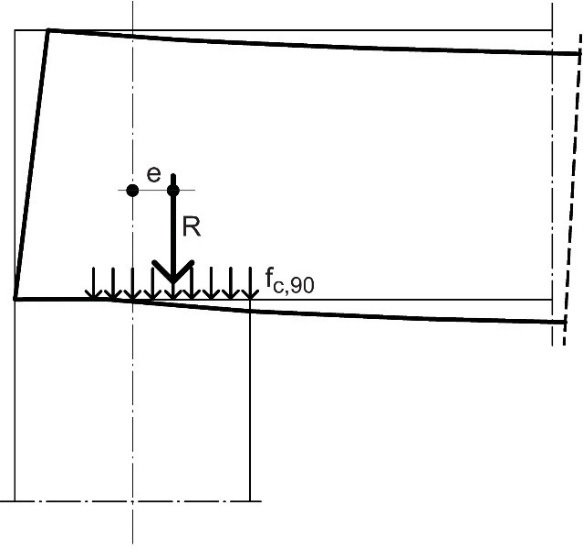
Figure 4.7 : Grande surface de contact entraînant une déformation non uniforme et des charges décentrées au niveau des appuis.
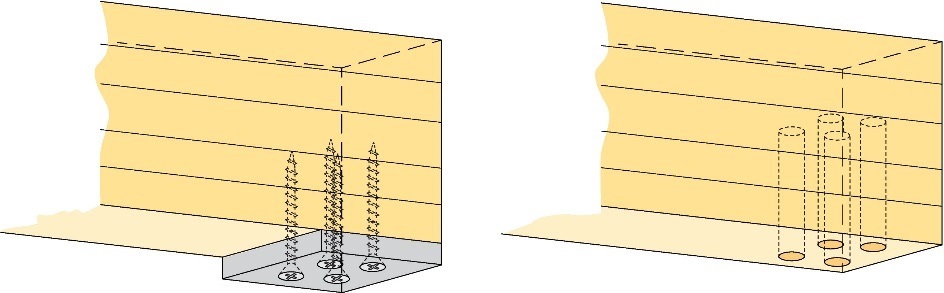
Figure 4.8 : Exemple d’un appui de poutre renforcé concernant la compression perpendiculaire au fil à l’aide de vis autotaraudeuses (à gauche) et de goujons collés (à droite).
L’approche de calcul concernant la compression perpendiculaire au fil consiste à satisfaire l’équation de dimensionnement suivante :

où :
σc,90,d correspond à la valeur de calcul de la contrainte de compression dans la surface de contact efficace perpendiculaire au fil
Fc,90,d correspond à la valeur de calcul de la charge de compression perpendiculaire au fil
Aef correspond à la surface de contact efficace en compression perpendiculaire au fil
kc,90 est un coefficient qui tient compte de la conditions limites, de la possibilité de fendage et d’un degré de déformation en compression
fc,90,d correspond à la valeur de calcul de la résistance à la compression perpendiculaire au fil

La surface de contact efficace Aef nécessaire pour calculer les contraintes existantes doit être déterminée en prenant en compte la longueur de contact efficace lef :

selon les notations utilisées dans la Figure 4.9.
Les valeurs de kc,90 pour différentes configurations sont indiquées dans le Tableau 4.4.
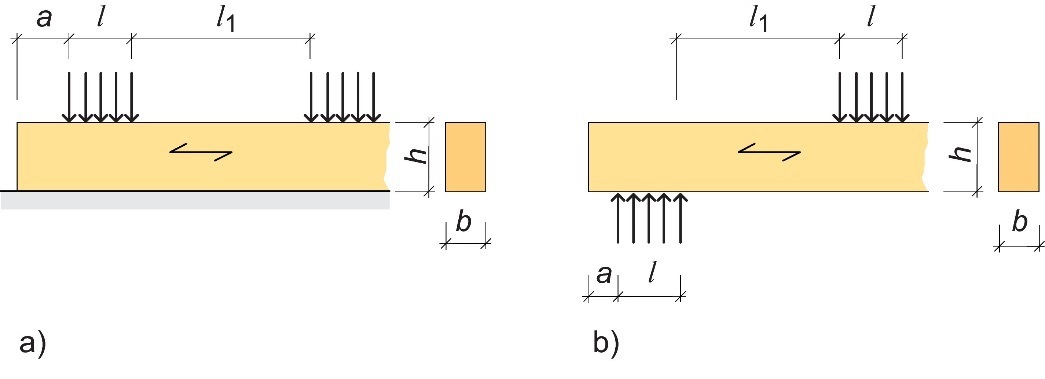
Figure 4.9 : Élément sur appui continu (a) ou sur appuis discrets (b) soumis à une compression perpendiculaire au fil.
Tableau 4.4 : valeurs du coefficient kc,90 selon le type d’appui et la distance l1 entre les charges. Les valeurs entre parenthèses correspondent au bois massif et les autres, au lamellé-collé. Notations selon la Figure 4.10.

Une série de charges concentrées proches (solives ou chevrons dont l’entraxe est < 610 mm par exemple) peut être considérée comme une charge répartie.
4.1.5. Contraintes de compression inclinées par rapport au fil
Les contraintes de compression à un angle α par rapport au fil doivent satisfaire l’équation suivante :
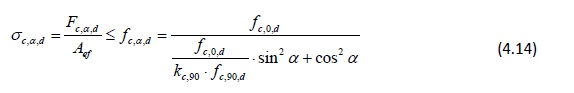
où :
σc,α,d est la valeur de calcul de la contrainte de compression à un angle α par rapport au fil du bois
σc,0,d est la valeur de calcul de la contrainte de compression dans le sens du fil
fc,α,d est la valeur de calcul de la résistance à la compression à un angle α du fil
fc,90,d est la valeur de calcul de la résistance à la compression perpendiculaire au fil
fc,0,d est la valeur de calcul de la résistance à la compression dans le sens du fil
Fc,α,d est à la valeur de calcul de la charge de compression à un angle α du fil
kc,90 est le coefficient d’amplification (cf. Figure 4.9)
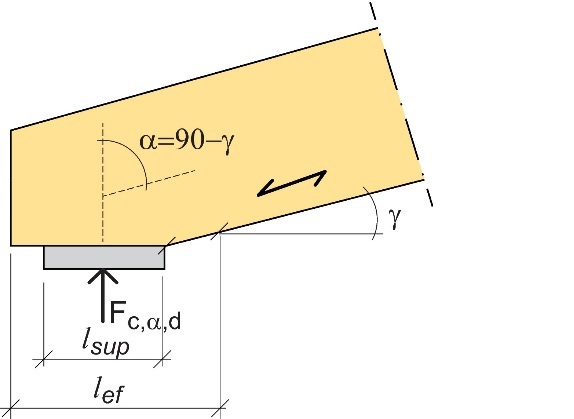
Figure 4.10 : Élément soumis à une compression à un angle α du fil.
4.2. FLAMBEMENT AXIAL
La base de la théorie des poteaux est l’approche d’Euler basée sur un poteau mathématiquement droit, prismatique, bi-articulé, parfaitement sollicité à l’axe et qui est suffisamment élancé pour flamber sans contrainte à n’importe quel point de la section transversale dépassant la limite du matériau. La charge de flambement se définie comme suit :

où E·I correspond à la rigidité en flexion et L à la longueur du poteau.
4.2.1. Longueurs de flambement
La charge d’Euler PE est la valeur de référence à laquelle la résistance d’un poteau réel est généralement comparée. S’il est possible de définir mathématiquement des conditions limites autres que des rotules parfaites, la charge critique est formulée comme suit :

où β·L correspond à une « longueur efficace » définissant la partie fléchie entre les points de courbure nulle. En d’autres termes, β·L correspond à la longueur de flambement d’un poteau bi-articulé équivalent soumis à la même charge qu’un poteau encastré.
La Figure 4.11 présente les valeurs théoriques de β dans des conditions idéales dans lesquelles les maintiens en rotation et/ou en translation aux extrémités du poteau sont soit pleins soit inexistants.
Au niveau du pied, la condition d’encastrement parfait est presque satisfaite seulement lorsque le poteau est rigidement fixé en pied et que la rotation est alors négligeable (cf. les conditions d’encastrement a, b, c et e représentées dans la Figure 4.11).
Au niveau de l’extrémité supérieure, les conditions d’encastrement a, c et f sont presque satisfaites lorsque la tête du poteau est intégralement encastrée dans une poutre beaucoup plus rigide que la tête du poteau. La condition d’encastrement c est identique à la condition a, si ce n’est qu’en haut, le maintien en translation est soit absent soit minimal. La condition f est identique à la condition c, si ce n’est qu’il n’y a aucun maintien en rotation en pied. Les valeurs de calcul recommandées pour β correspondent à une modification des valeurs idéales, en tenant compte du fait que ni un encastrement parfait ni une rigidité parfaite ne sont possibles dans la pratique.
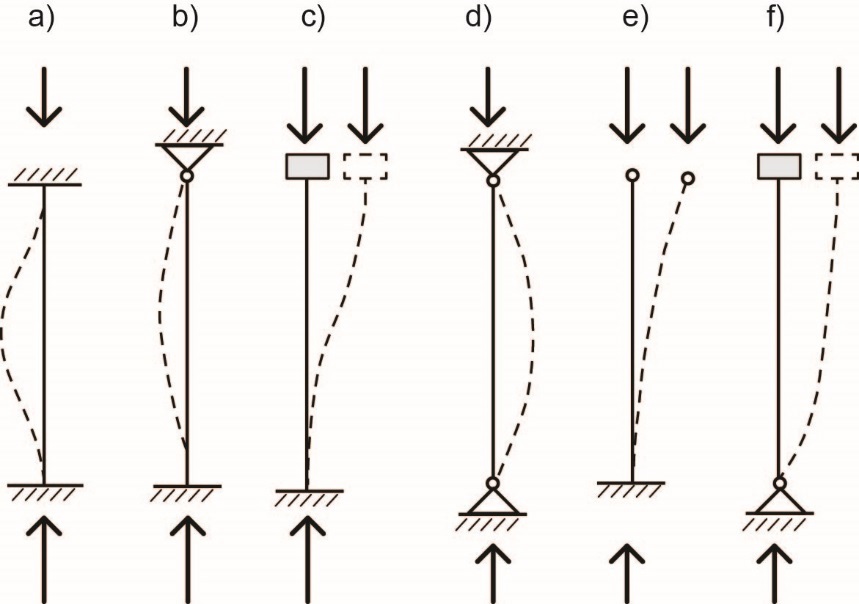

Figure 4.11 : Longueurs de flambement applicables aux poteaux en théorie et en pratique dans différentes conditions limites.
Le principe consistant à utiliser la longueur de flambement pour déterminer la charge de flambement critique d’un élément comprimé peut également s’appliquer aux poteaux non prismatiques, aux poteaux se caractérisant par une charge de compression non uniforme et aux poteaux dotés de maintiens élastiques.
4.2.2. Approche de calcul
Les imperfections géométriques, qui se traduisent par une déformation linéaire inévitable du poteau et/ou une charge axiale décentrée, introduisent une flexion complémentaire à la sollicitation de compression axiale. Des flèches latérales apparaissent dès le début de la sollicitation et la charge de rupture est atteinte lorsque la capacité résistante interne au niveau de la section critique est égale au moment d’excentricité induit (produit de la charge par la flèche). La charge de rupture dépend donc des imperfections. Il convient généralement de prendre en compte les imperfections géométriques ainsi que les caractéristiques du matériau (masse volumique, présence de nœuds, teneur en humidité, etc.) pour déterminer la résistance des poteaux en bois.
En première approche, un poteau peut être conçu à l’aide d’une analyse au second ordre simplifiée. Il convient à cette fin de définir une valeur initiale δ0 correspondant à la déformation linéaire initiale. Dans le cas des structures en bois lamellé-collé, δ0 est généralement égal à L/500, L correspondant à la longueur de l’élément comprimé. Dans le cas d’un poteau bi-articulé soumis à une charge de compression centrée P, le calcul peut tenir compte de l’interaction des contraintes de compression σ(P) et des contraintes de flexion σ(M) (cf. Figure 4.12).
Le déplacement latéral additionnel induit par P est représenté par δp. Le déplacement latéral total δtot peut être défini par :

où Pcr correspond à la charge de flambement (théorique). Le moment de flexion peut ensuite être calculé comme le produit de la charge axiale appliquée P et de la déformation latérale finale :
M = P·(δ0 + δp) (4.18)
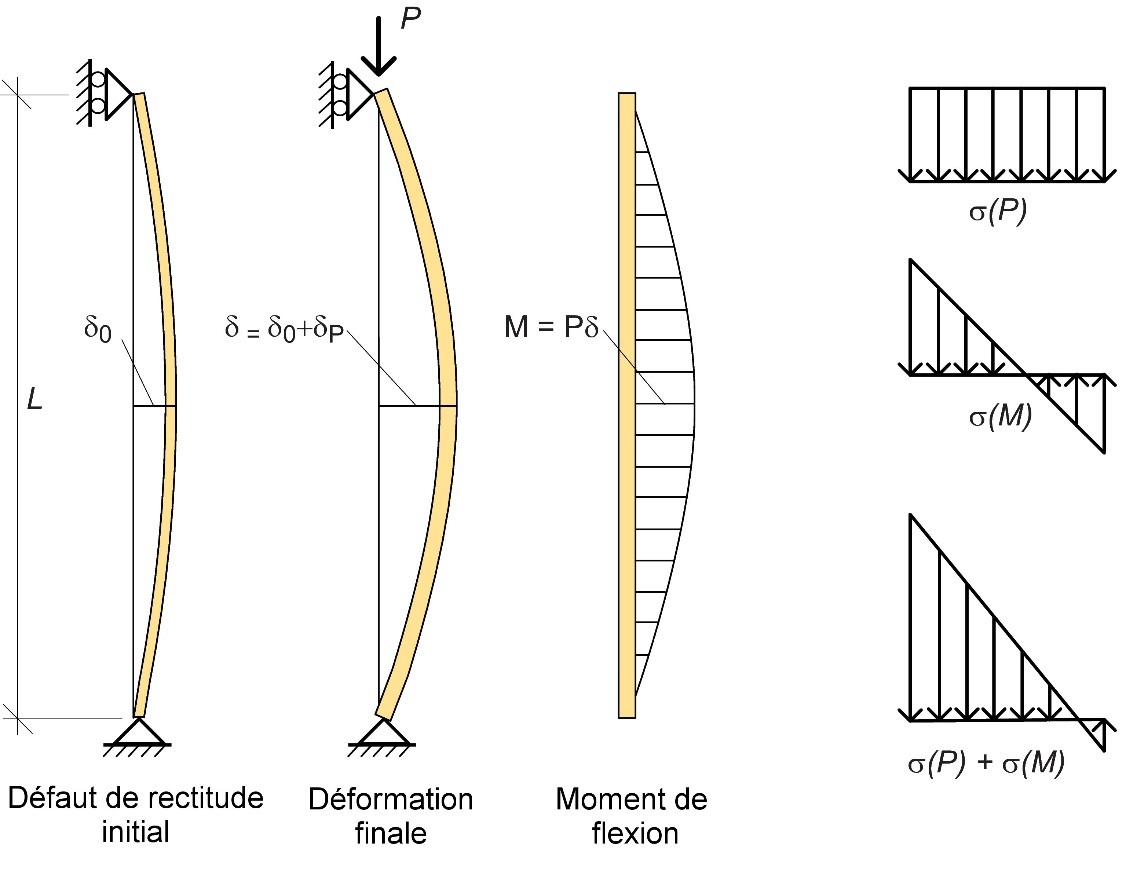
Figure 4.12 : Flambement d’un poteau en bois considéré comme un problème non linéaire (au second ordre).
Il convient ensuite de vérifier que l’effet combiné des contraintes de compression et de la contrainte de flexion ne dépasse pas la valeur de calcul de la résistance du bois lamellécollé.
Cette approche ne prend cependant pas en compte plusieurs facteurs importants, et notamment le risque de rupture du bois en cas de contraintes de compression importantes.
4.2.3. Compression axiale pure (conformément à l’Eurocode 5)
Les différentes parties de cette section expliquent comment déterminer la résistance minimum requise pour un poteau lamellé-collé conformément à l’Eurocode 5 (EC5). De même que pour les autres Eurocodes, la conception des poteaux conformément à l’EC5 repose sur l’analyse de flambement linéaire. Les effets non linéaires (ou au second ordre) sont pris en compte dans le calcul par l’introduction d’un coefficient de réduction (de la résistance) kc. La condition à satisfaire est la suivante :

Où
fc,d correspond à la valeur de calcul de la résistance à la compression
A correspond à l’aire de la section transversale totale du poteau
kc est un coefficient de réduction prenant en compte le risque de flambement
L’équation qui permet de calculer kc a été établie à partir des simulations numériques d’un grand nombre de poteaux présentant différentes imperfections en termes de propriétés géométriques et matérielles, basées sur l’observation de poteaux réels. La plasticité du bois sur le côté comprimé a également été prise en compte dans ces simulations numériques.
Dans les codes de conception modernes, l’expression relative aux valeurs de kc est donnée en fonction du rapport d’élancement relatif 

Où
fc,0,k correspond à la valeur caractéristique de la résistance à la compression parallèle au fil du bois
E0,05 correspond à la valeur du fractile à 5 % du module d’élasticité parallèle au fil 
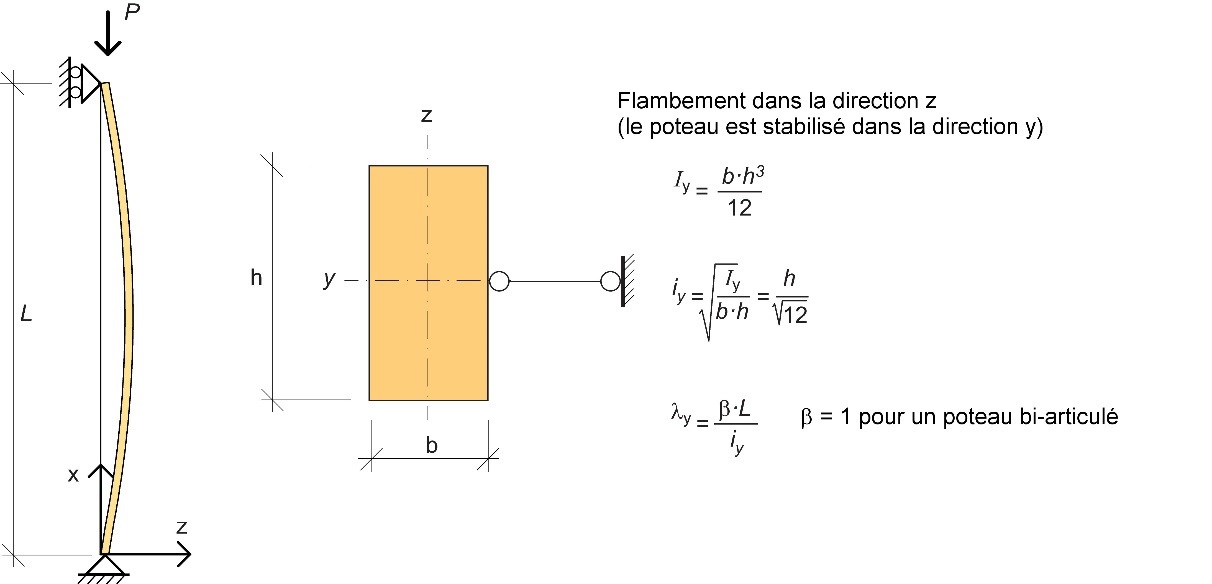
Figure 4.13 : Flambement d’un poteau en bois : définition du moment d’inertie (I), du rayon de giration (i) et de l’élancement
des poteaux
L’expression relative au coefficient de réduction kc en fonction du rapport d’élancement relatif 
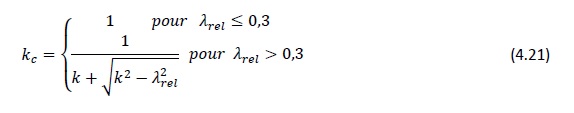
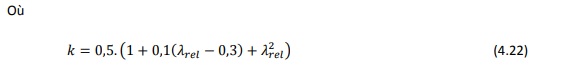
La relation entre kc et le rapport d’élancement 
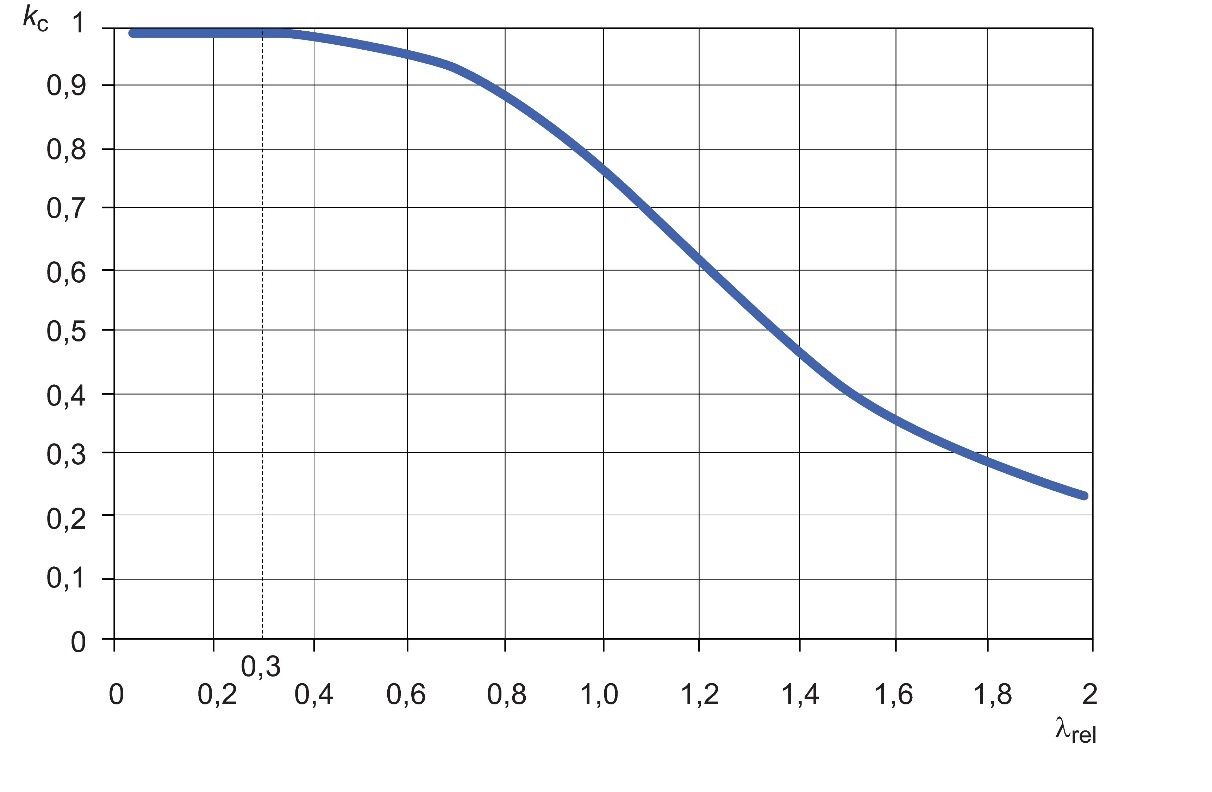
Figure 4.14 : Coefficient de réduction kc en fonction du rapport d’élancement relatif 
Dans la pratique, il convient d’éviter que le rapport relatif d’élancement 
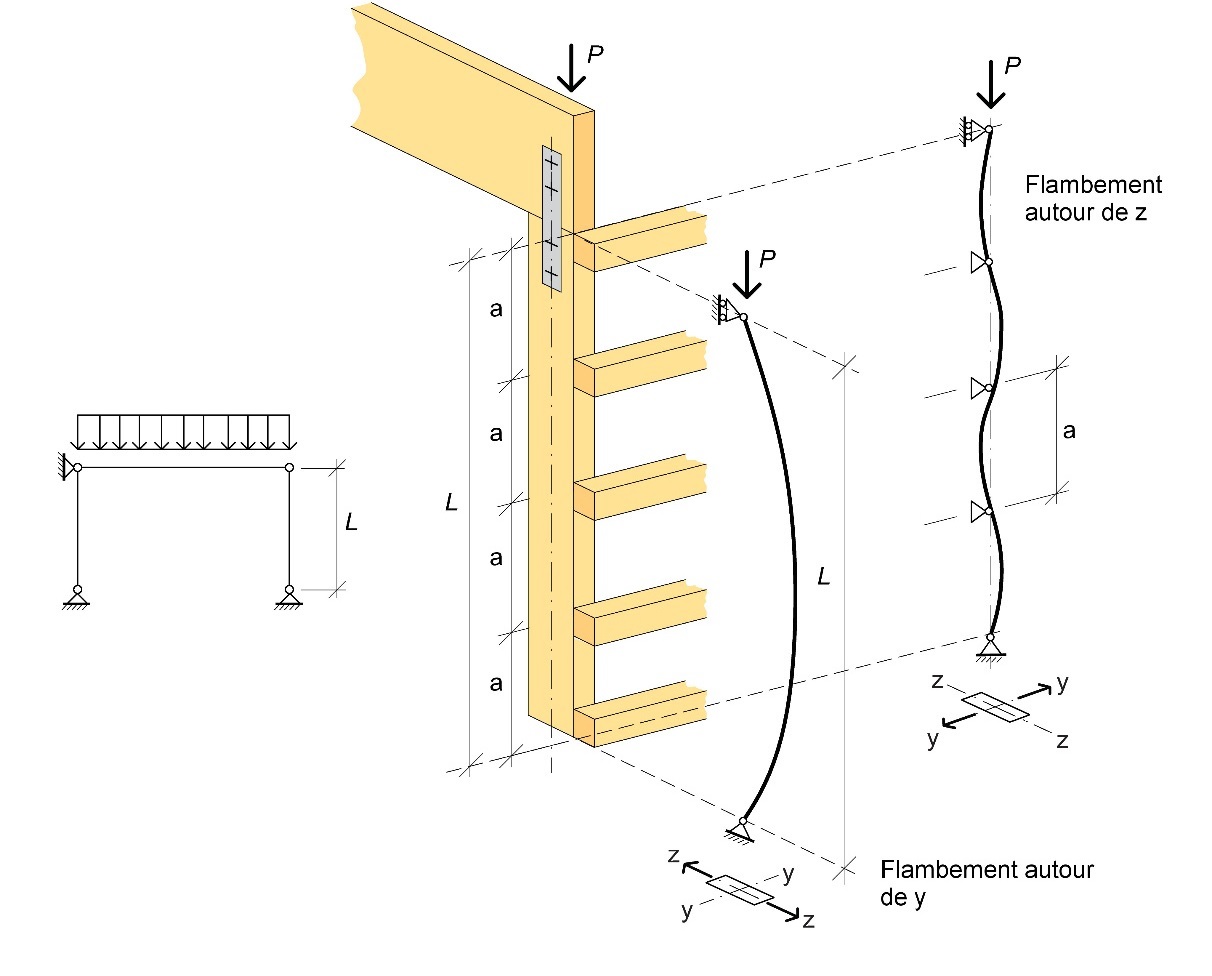
Figure 4.15 : Flambement d’un poteau en bois dans un mur extérieur
En haut et en bas des poteaux ainsi qu’aux différents endroits où la section transversale est affaiblie par des trous ou percements, notamment, il convient de démontrer que :

où Anet correspond à l’aire de la section transversale nette du poteau.
4.2.4. Flexion et compression axiale combinées
Lorsqu’aucune instabilité en torsion latérale ne peut se produire, deux modes de ruptures sont susceptibles d’intervenir :
a) λrel ≤ 0,3 – le comportement au flambement n’est pas pertinent et la rupture sera basée sur la résistance à la compression de l’élément ;
b) λrel > 0,3 – un flambement peut intervenir et la rupture sera basée sur la résistance à la compression de l’élément multipliée par le coefficient de réduction (basé sur l’instabilité) qui lui est associée, c’est-à-dire kc.
En théorie, un élément en bois peut subir une compression axiale et une flexion déviée. Les cas de charges les plus courants où la compression et la flexion interviennent simultanément sont ceux illustrés par la Figure 4.16. Seuls ces cas seront abordés dans les paragraphes ci-après.
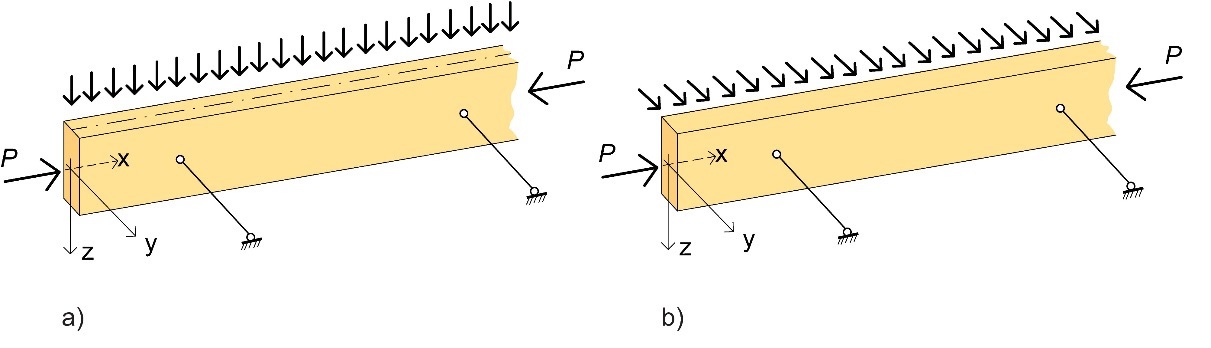
Figure 4.16 : Interaction de la flexion et de la force axiale. (a) Flexion selon l’axe fort (y). (b) Flexion selon l’axe faible (z).
4.2.4.1. Cas : λrel ≤ 0,3
En l’absence de réduction de la résistance due au flambement, il est possible de tirer profit des avantages de la résistance associés au comportement plastique du bois lorsqu’il est soumis à des contraintes de compression. Les conditions de calcul sont les suivantes :

où :
σc,0,d correspond à la valeur de calcul de la contrainte de compression
σm,y,d et σm,z,d correspondent respectivement aux valeurs de calcul des contraintes de flexion selon les axes y et z
fc,0,d correspond à la valeur de calcul de la résistance à la compression dans le sens du fil
fm,y,d et fm,z,d correspondent respectivement aux valeurs de calcul des résistances à la flexion selon les axes y et z.
La Figure 4.17 montre le diagramme d’interaction pour un élément sollicité par un moment de flexion et une compression axiale combinés selon l’application de la théorie plastique. Lorsque la théorie plastique s’applique, le matériau cède lorsqu’il atteint la résistance à la compression, permettant à la contrainte dans la section de s’étendre jusqu’à la surface et d’améliorer sa résistance.
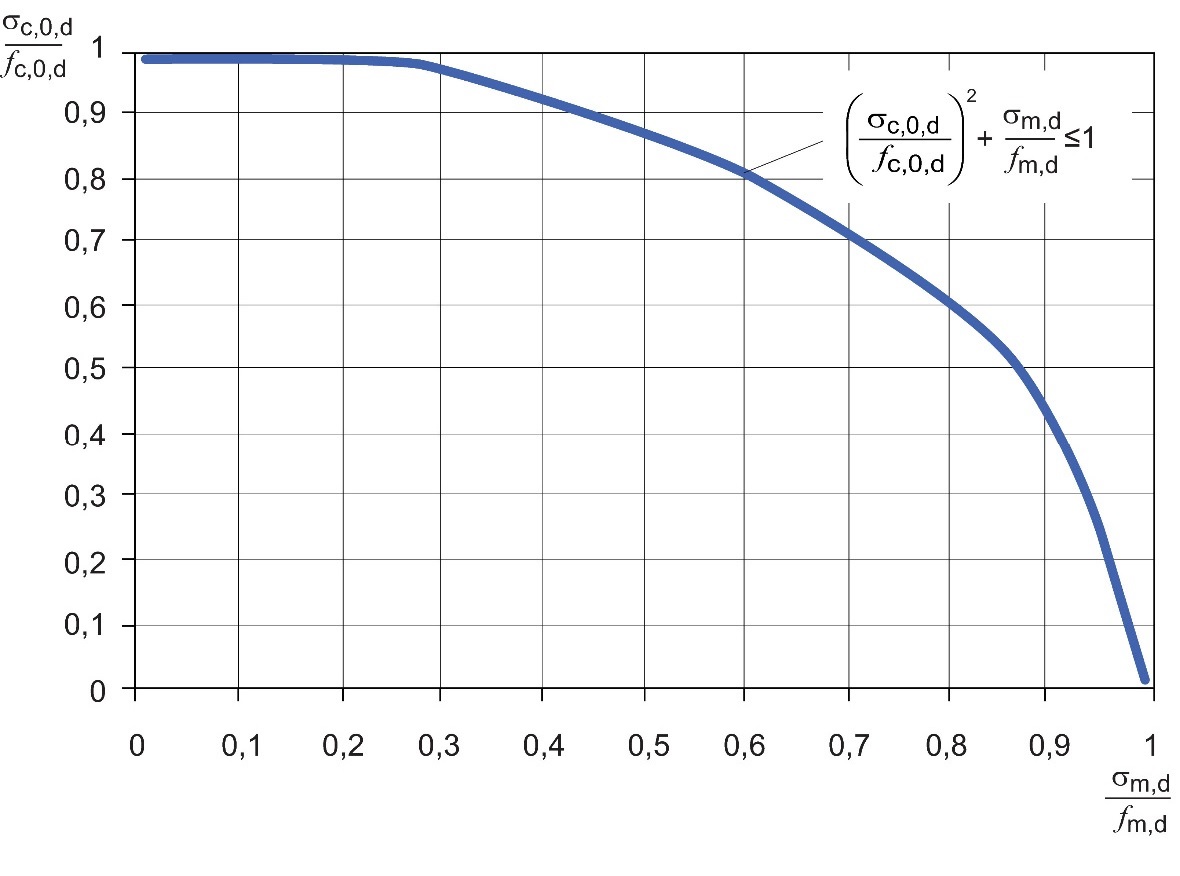
Figure 4.17 : Diagramme d’interaction pour un élément soumis à une flexion et à une compression axiale combinées selon
un axe, avec λrel ≤ 0,3. L’indice m,d est utilisé comme une valeur générique ; il désigne la contrainte de flexion et la résistance
à la flexion induites par un moment de flexion autour de l’axe y ou de l’axe z. L’indice c,0,d correspond à la compression
axiale.
4.2.4.2. Cas : λrel > 0,3
Dans ce cas, étant donné que les effets du flambement par chargement axial doivent être pris en compte, aucun avantage n’est retiré du comportement plastique de l’élément et la charge limite est atteinte lorsque le matériau parvient à sa résistance de rupture dans la fibre extrême. Les conditions de calcul sont les suivantes :
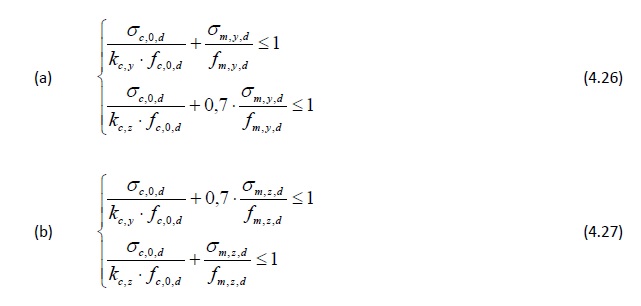
où :
kc,y et kc,z sont les coefficients de réduction prenant en compte le risque de flambement (cf. Éq. 4.21).
Les indices « y » et « z » indiquent que le flambement intervient selon l’axe y ou l’axe z.
À noter que le coefficient de réduction kc est déterminé à partir du rapport d’élancement pour le flambement intervenant dans la direction la moins favorable, quelle que soit la direction dans laquelle le moment agit.
La Figure 4.18 montre le diagramme d’interaction pour un élément sollicité par un moment de flexion et une compression axiale combinés selon l’application de la théorie de l’élasticité.
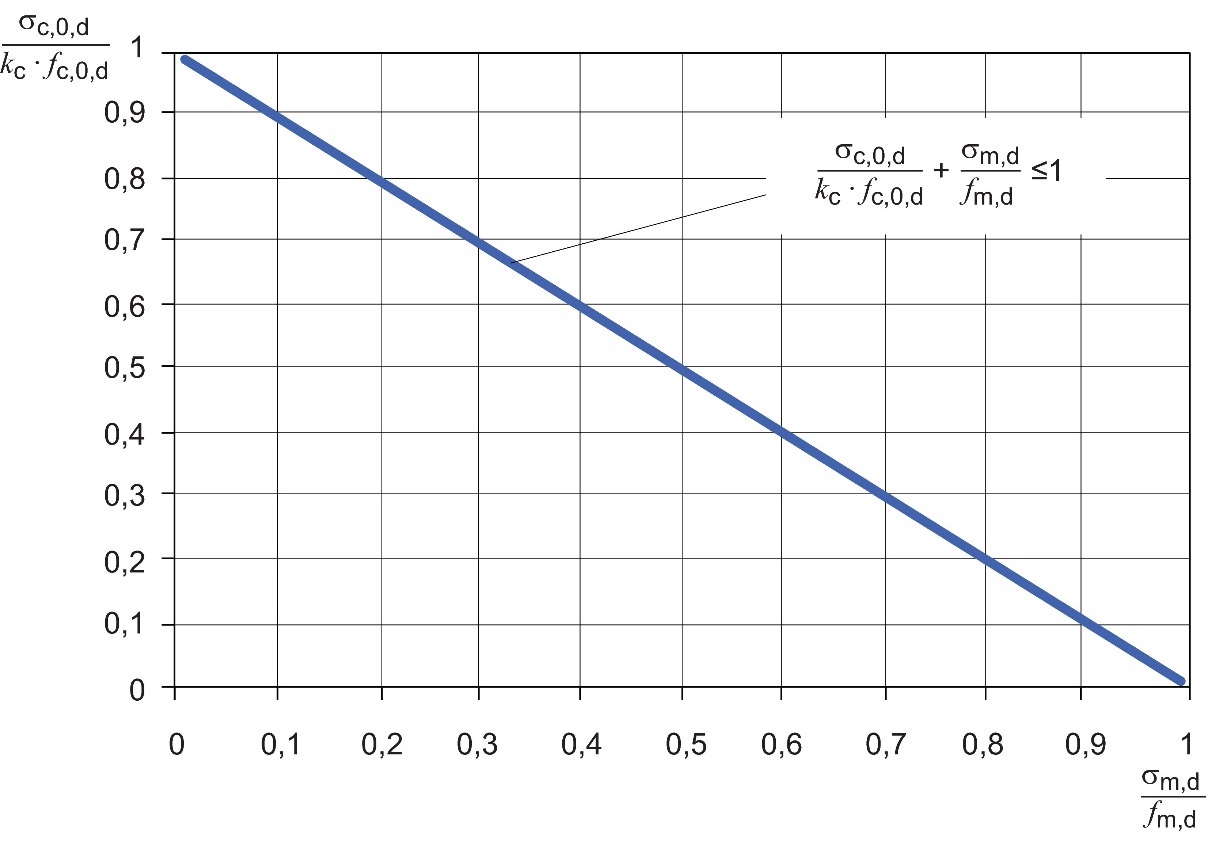
Figure 4.18 : Diagramme d’interaction pour un élément soumis à une flexion et à une compression axiale combinées selon un axe, avec λrel > 0,3. Conditions élastiques. L’indice m,d est utilisé comme une valeur générique ; il désigne la contrainte de flexion et la résistance à la flexion induites par un moment de flexion autour de l’axe y ou de l’axe z. L’indice c,0,d correspond à la compression axiale.

