VOLUME 2 - 6. ETATS LIMITES DE SERVICE

Contrairement aux aspects liés à la résistance, il est très rare que les aspects liés à l’aptitude au service (fonctionnalité, apparence, confort des usagers) puissent entraîner à eux seuls l’effondrement d’un élément ou d’une structure. Ils sont néanmoins très importants en termes de conception pour un certain nombre de raisons, et notamment :

pour maintenir les exigences relatives à l’aspect visuel et à la fonctionnalité de l’élément ou de la structure dans des limites acceptables,
pour éviter la dégradation des finitions fragiles (plâtre, papier peint et peinture),
afin que la flèche des charpentes de comble ne soit pas excessive et que des flaques d’eau de pluie, par exemple, ne provoquent pas de fuite à travers la structure,
pour limiter les effets du fluage,
pour conférer une rigidité suffisante à la structure, afin que les vibrations n’entraînent pas de problèmes de confort.

6.1. EXIGENCES DE PERFORMANCES

Il convient de limiter les flèches et les mouvements dans un bâtiment afin d’éviter toute dégradation et tout autre effet indésirable en service. Un bâtiment doit être suffisamment résistant pour supporter les charges maximales attendues avec un coefficient de sécurité approprié. Les structures conçues pour l’état limite ultime sont souvent relativement élancées, ce qui signifie qu’elles peuvent être sujettes à d’importantes déformations. Les critères d’aptitude au service utilisés lors de la conception sont donc très importants, en particulier pour les structures légères telles que celles en bois et en lamellé-collé.

Dans la plupart des cas, les exigences relatives à l’aptitude au service sont déterminantes dans le cadre de la conception. Il est donc important que l’amplitude des déformations puisse être prévue avec suffisamment de précision et que les exigences et les limites soient correctement définies. Or ceci constitue un problème dans le cadre de la conception actuelle, car les connaissances relatives aux exigences et aux méthodes de prévision sont souvent insuffisantes .

Les structures en bois se caractérisent par des flèches relativement importantes lorsqu’elles sont soumises à une charge prolongée. Le bois étant un matériau anisotrope, le type de réponse varie en fonction du mode de sollicitation. La sensibilité aux changements environnementaux (jeux du bois liés à l’humidité, par exemple) a également un effet important sur la déformation des systèmes structuraux en bois lamellé-collé.

Il convient de tenir compte de la déformation à long terme (fluage) ainsi que des effets environnementaux au moment d’étudier le comportement en service des structures en bois lamellé-collé. Les exigences relatives à l’aptitude au service doivent normalement être définies par le client en accord avec l’entrepreneur, et non par les codes. Les codes posent néanmoins des bases – principes généraux concernant les charges, propriétés des matériaux et méthodes de calcul –, qui peuvent être utilisées dans le cadre du calcul aux états limites de service.

Lorsqu’elle est excessive, la flèche des composants structuraux peut entraîner une détérioration des éléments structuraux et non structuraux, des effets négatifs sur l’utilisation et divers effets perçus comme désagréables par les personnes qui occupent le bâtiment.

La déformation d’un élément structural ne provoque que rarement la rupture de ce seul élément, à l’exception des déformations liées au système de stabilisation. Si un certain nombre d’éléments présentent des déformations relativement importantes – ou si la déformation d’un élément entraîne des mouvements dans d’autres éléments –, cela peut provoquer une modification du système structural primaire ou une instabilité de la structure dans son intégralité. Ces effets système peuvent également induire des effets inacceptables sur le plan de l’aptitude au service. Il est donc intéressant non seulement d’étudier le comportement de chaque élément, mais aussi de tenir compte du système dans son intégralité (assemblages y compris) au moment d’analyser la déformation. Ce type d’analyse est cependant relativement complexe et n’est donc réalisé que dans des cas très spécifiques.

Les déformations peuvent avoir différents effets défavorables sur l’utilisation du bâtiment. Elles peuvent par exemple entraîner une inclinaison insuffisante des toitures et des problèmes liés à l’ouverture des portes et des fenêtres. Les flèches peuvent aussi être source de problème dans le cas des édifices spéciaux, tels que les gymnases ou les locaux soumis à des exigences élevées concernant le caractère plat d’une surface (en raison d’un équipement sensible, par exemple). Les limites d’aptitude au service doivent également être appliquées aux bâtiments et à leurs composants afin d’éviter que les éléments non structuraux soient inclus dans le cheminement des charges.

En cas de flèches excessives, une structure perd de son attrait et peut susciter un sentiment d’insécurité. Ces observations sont subjectives ; les flèches ne risquent pas de mettre en danger la structure ou de réduire sa durée de vie, mais il convient de les limiter pour maintenir la confiance de l’usager. Ces limites concernent davantage les flèches à long terme que les flèches à court terme, récupérables, pouvant survenir en raison de pics de charges élevés.

Il ressort des précédentes observations que la limitation de la déformation est à prendre en compte dans de nombreuses situations différentes pour diverses raisons plus ou moins importantes. Pour des raisons pratiques, deux catégories principales de contrôle de la déformation sont définies : 1) éviter tout endommagement permanent et 2) conférer un aspect et une utilité générale satisfaisants. Le concepteur peut classer chaque cas particulier dans l’une de ces catégories.

Les problèmes liés à l’aptitude au service incluent également des vibrations de différentes origines. Les vibrations dues aux pas et/ou à différents types de machines peuvent être source d’inconfort pour les personnes, mais aussi de problèmes pour les équipements sensibles et le comportement structural. Dans ces cas, les exigences sont souvent encore plus complexes qu’en cas de flèche statique. Les observations relatives à la déformation statique s’appliquent néanmoins dans de nombreux cas, car c’est l’utilisation de la structure qui permet de déterminer les vibrations acceptables.

6.2. DEFORMATIONS STATIQUES

Pour la plupart des structures, les charges consistent en des charges permanentes G_i et en des charges variables Q_i. Dans le cas des structures en bois et en lamellé-collé, souvent dominées par des charges variables, l’ampleur de la flèche varie considérablement au cours de la durée de vie de la structure.

La Figure 6.1 illustre le comportement en déformation d’une poutre soumise à une charge permanente G et à une charge de neige Q. La flèche totale peut être subdivisée en une partie w₁, induite par la charge permanente immédiatement après la sollicitation, et en une partie w₂, variable au cours de la durée de vie de la structure. La partie variable w₂ consiste en une portion réversible w_2,inst, qui n’est présente que lorsque la charge variable est présente, et en un fluage de la portion sans cesse croissant, qui peut être considéré en pratique comme irréversible. Les pics de charges de courte durée, tels que ceux illustrés dans la Figure 6.1, concernent à la fois la charge de neige et les charges (d’exploitation) imposées dans les bâtiments les plus courants.

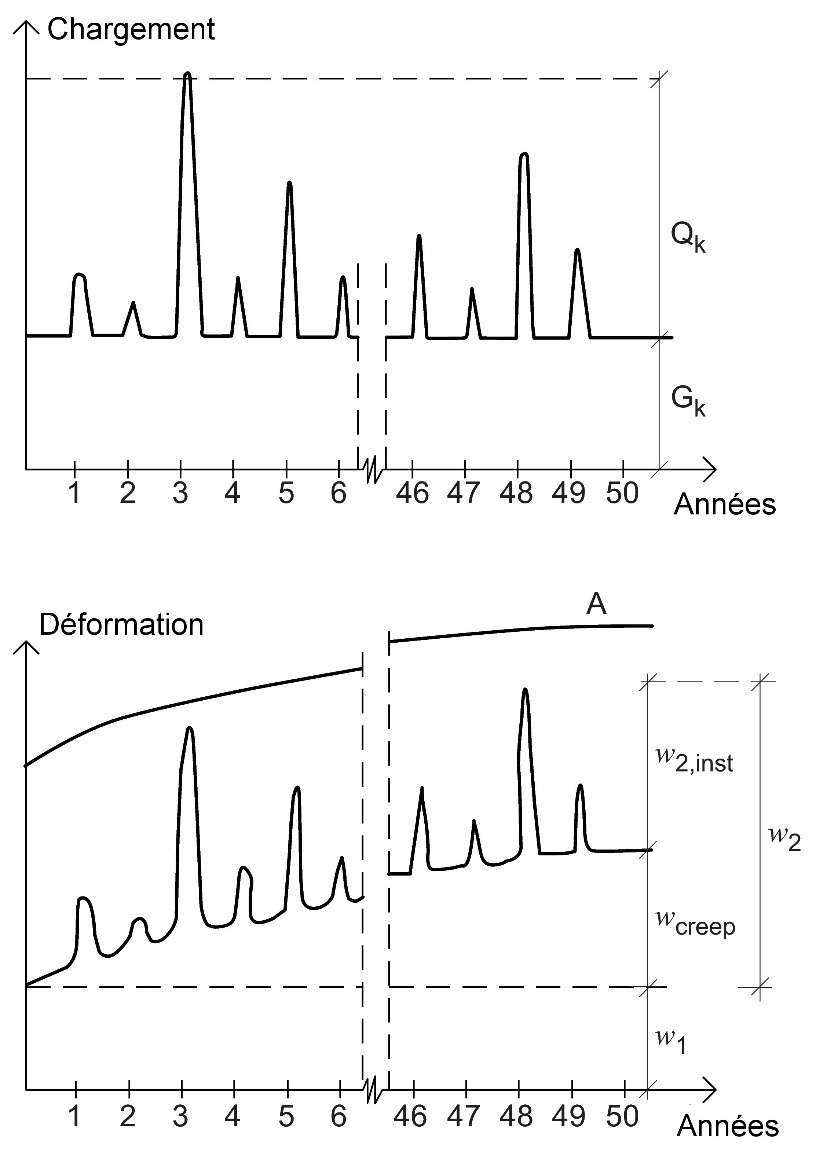
Figure 6.1 : Variation en fonction du temps de la flèche (figure du bas) d’une poutre soumise à des charges permanentes et
variables (figure du haut). La courbe A montre la flèche de fluage lorsque la poutre est soumise à des charges
caractéristiques G_k + Q_k pendant toute la période.

6.2.1. Déformations

La Figure 6.2 illustre le principe de déformation d’une poutre en bois ou en lamellé-collé pour montrer les différentes parties de la flèche. On peut supposer que la poutre est dotée d’une contre-flèche (ce qui peut être le cas d’une poutre lamellée-collée), w_c. Des pics de charges élevés surviennent pendant de courtes périodes, induisant une importante flèche w_inst. Cette flèche peut intervenir à tout moment au cours de la durée de vie de la structure.

Une partie de la charge sera prolongée pendant une période plus longue et entraînera une augmentation graduelle de la flèche, w_creep. Afin de déterminer la flèche totale après une longue période, wnet,fin, il est possible de calculer la somme de w_c, w_inst et w_creep.

La valeur du module d’élasticité – et, parfois, du module de cisaillement – est utilisée dans le calcul des déformations. Le plus raisonnable à l’état limite de service consiste à utiliser la valeur moyenne de chaque module.

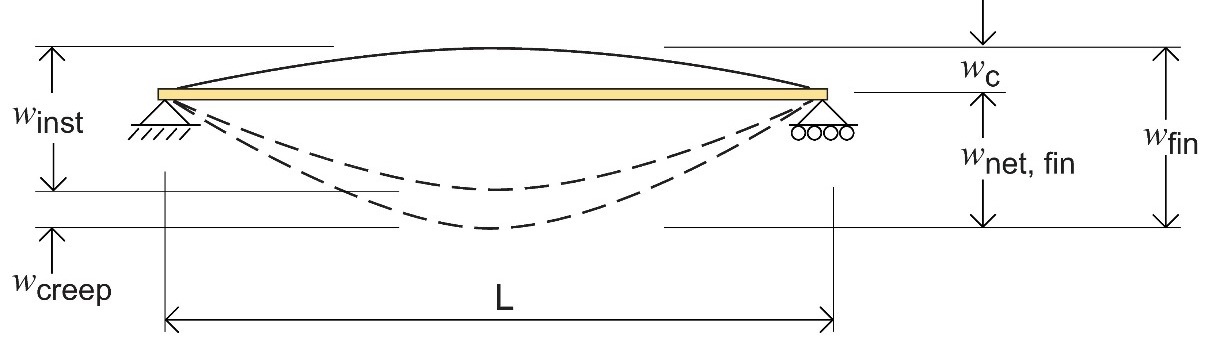
Figure 6.2 : Définitions des flèches.

Lorsqu’un élément travaille en flexion, il subit une déformation due non seulement à l’effet du moment de flexion, mais aussi à l’effet des forces de cisaillement, l’importance de la déformation de cisaillement dépendant principalement du rapport entre le module d’élasticité E de l’élément et son module de cisaillement ainsi que du rapport hauteur/portée. Prenons l’exemple d’une poutre rectangulaire en appui simple de hauteur h et de portée théorique L supportant une charge concentrée à mi-travée. Le rapport entre la flèche instantanée à mi-portée induite par les forces de cisaillement, w_inst,s, et la flèche instantanée à mi-portée induite par le moment de flexion, w_inst,m, est le suivant :

Dans le cas du lamellé-collé, E/G équivaut environ à 20 et pour le calcul pratique de la poutre, h/L varie entre 0,1 et 0,05, ce qui se traduit par une déformation de cisaillement comprise entre 5 et 20 % de la valeur de flexion. Ceci prouve qu’il est parfois judicieux de prendre en compte ces déformations lors de la conception des structures en bois lamellécollé.

Le tassement d’une structure constitue un cas de déformation particulier. Ce phénomène est généralement traité (dans l’Eurocode par exemple) comme un problème de conception à l’état limite ultime, à savoir qu’il implique une vérification des contraintes de compression au niveau des surfaces de contact où le bois lamellé-collé est soumis à une compression perpendiculaire au fil. Dans la pratique néanmoins, il s’agit souvent d’un problème d’aptitude au service, l’attention devant porter sur le tassement au niveau des assemblages plutôt que sur la rupture réelle de l’assemblage. Dans le cas d’un bâtiment en bois à plusieurs étages, des forces de grande amplitude peuvent intervenir dans les étages inférieurs et au niveau des fondations. Les forces de compression perpendiculaires au fil induisent des déformations susceptibles de devenir relativement importantes, notamment en comparaison des déformations parallèles au fil.

6.2.2. Effets à long terme et effets climatiques

Le comportement au fluage – c’est-à-dire l’augmentation au fil du temps de la flèche – des produits du bois et à base de bois est conditionné par plusieurs facteurs. L’amplitude du fluage dépend du taux d’humidité et de son amplitude de variation : plus ceux-ci sont élevés, plus le fluage est important (cf. Figure 6.3).

Même lorsque les niveaux d’humidité sont relativement bas, les variations de la teneur en humidité entraînent des augmentations plus importantes qu’en cas d’humidité élevée constante. Il est donc important de tenter d’estimer la teneur en humidité et les variations d’humidité de l’air environnant pendant la durée de vie de la structure.

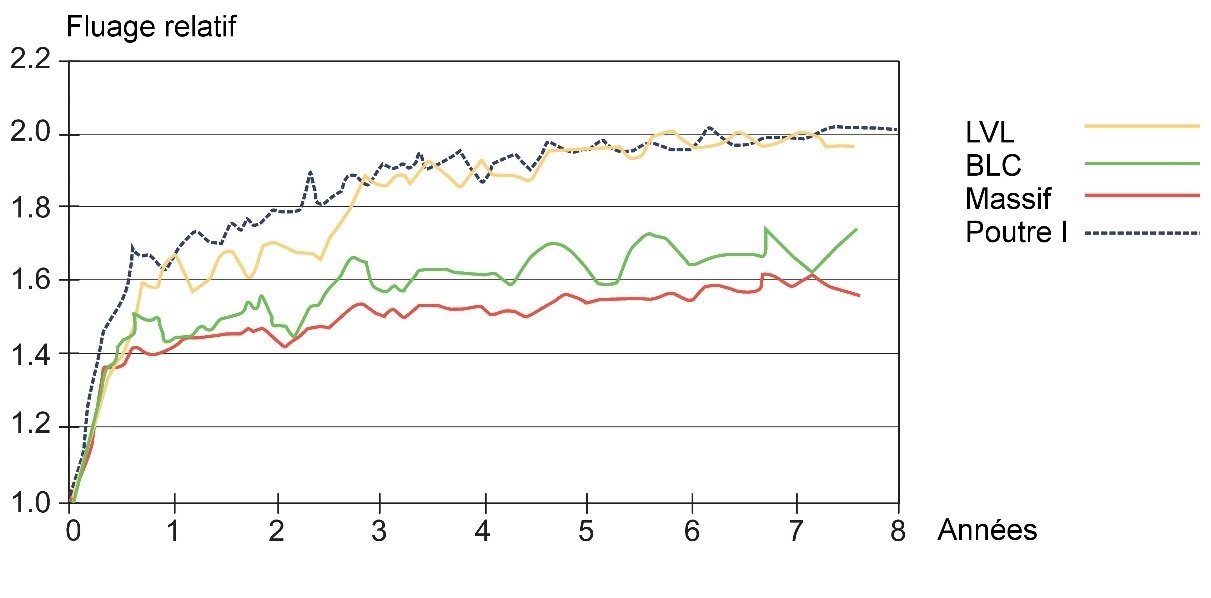
Figure 6.3 : Fluage relatif dans un environnement protégé. (Fluage relatif = flèche de la poutre au temps t/flèche initiale) Niveau de contrainte 2 MPa. D’après Ranta-Maunus,& Kortesmaa, 2000.

Outre les effets du fluage pur sous charge constante et du fluage dû aux variations d’humidité, des effets résultent des différents niveaux de charges auxquels est soumise la structure pendant sa durée de vie. Tous ces effets doivent être pris en compte dans le processus de conception.

En principe, le comportement du bois soumis à une compression perpendiculaire au fil est le même que celui d’une poutre, mais inclut quelques effets supplémentaires. Dans ce cas, la déformation est amplifiée par le retrait du bois perpendiculaire au fil, qui est beaucoup plus important que le retrait parallèle au fil (lequel est négligeable). Les effets du fluage sont également plus importants que pour une poutre qui travaille en flexion.

Dans le cas d’un bâtiment soumis à une charge constante pendant toute sa durée de vie, le rapport entre la flèche instantanée (winst) et la flèche de fluage (wcreep) est le suivant :

où k_def correspond à un coefficient de déformation dont la valeur dépend du matériau sollicité ainsi que de sa teneur en humidité et des variations d’humidité.

Dans le cas des structures ou des éléments conformes aux conditions ci-dessus, la déformation finale w_fin peut être formulée comme suit :

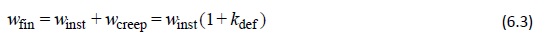
La déformation finale sous charge permanente et sous charge variable est alors définie comme suit :

Pour les actions permanentes G, lorsque la charge est instantanée :

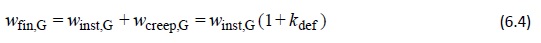
Pour les actions variables, Q_i :

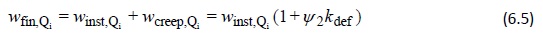
La valeur de k_def est déterminée en fonction des conditions climatiques. Étant donné que les effets du fluage dépendent aussi de la durée de la charge ou, en d’autres termes, de la valeur moyenne de la charge, le coefficient ψ₂ est introduit pour permettre la description de cet effet (ψ₂= 1 pour une charge constante). Les valeurs de k_def et de ψ₂ reposent sur des résultats expérimentaux, mais les chiffres comportent des incertitudes relativement importantes. La valeur de k_def augmente proportionnellement à l’humidité de l’air environnant. La valeur de ψ₂ augmente avec la durée de charge. Il est donc essentiel de se rappeler que les variations d’humidité sont tout aussi importantes que les valeurs maximale et moyenne de l’humidité relative. Si l’on peut raisonnablement supposer que d’importantes variations d’humidité se produiront au fil du temps, il peut être intéressant d’appliquer une classe de service plus stricte que lorsque seule la valeur maximale de l’humidité est utilisée.

Dans le cadre de l’analyse de la déformation finale, la sollicitation est la même que celle utilisée pour la déformation instantanée et l’effet du fluage sur le comportement lié au déplacement est déterminé à l’aide des propriétés de la rigidité réduite :

où E_fin correspond à la valeur finale moyenne du module d’élasticité, E correspond à la valeur nominale moyenne du module d’élasticité et k_def correspond au coefficient de déformation pour le bois et les produits à base de bois.

6.2.3. Combinaisons d’actions

Au moment de calculer la déformation conformément aux précédentes sections, il convient de définir les charges à prendre en compte. Trois combinaisons d’actions différentes peuvent être formulées afin de définir les combinaisons d’actions pertinentes. Les formules correspondent à un cas général de charges variables Q_k,i.

Combinaisons caractéristiques

où ψ0,iQk,i correspond à la valeur de combinaison caractéristique de la charge variable.

Cette combinaison donne une valeur élevée de la charge et peut normalement être utilisée pour déterminer la flèche à court terme w2,inst.

Combinaisons fréquentes

où ψ_1,1Q_k,1 correspond à la valeur fréquente de la charge Q_k,1 et ψ_2,iQ_k,i correspond à la valeur quasi-permanente de la charge variable Qk,i. Il s’agit de la combinaison à utiliser pour évaluer les effets réversibles, c’est-à-dire les effets qui se produisent à certaines fréquences, mais qui diminuent lorsque les charges diminuent.

Combinaison quasi-permanente

La valeur ψ_2,iQ_k,i est la valeur quasi-permanente de la charge variable Q_k,i. Il s’agit de la combinaison à utiliser pour évaluer les effets (du fluage) à long terme.

Si les équations 6.3 à 6.5 et 6.7 à 6.9 sont utilisées, la déformation finale sous charge permanente et sous charge variable est définie comme suit :

Pour les actions permanentes G :

Il est important de noter que cette combinaison de charges donne des valeurs élevées pour la déformation totale, car la déformation due à la charge variable est calculée en fonction de la valeur caractéristique. Ceci est satisfaisant lorsque le contrôle de la flèche concerne un endommagement permanent dans la mesure où l’effet des charges élevées de courte durée est alors intéressant.

En cas de contrôle relatif à l’aspect et à l’utilité, il peut s’avérer plus judicieux de calculer la flèche en fonction de la combinaison d’actions fréquente (Éq. 608) ou de la combinaison d’actions quasi-permanente (Éq. 6.9). Les formules 6.11 et 6.12 permettant de calculer la déformation finale due à des charges variables sont alors modifiées. En prenant par exemple comme base la combinaison d’actions fréquente, on obtient :

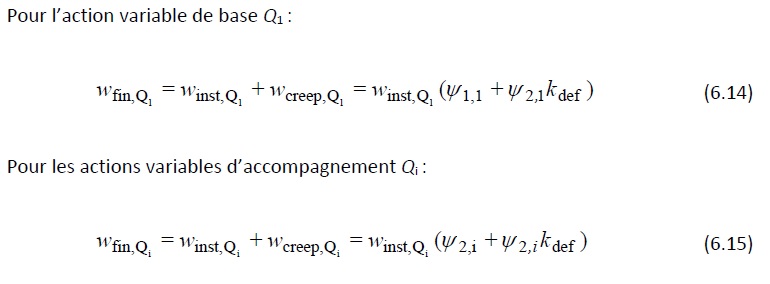
6.2.4. Limitation des déformations

Il est possible de déterminer une limite de flèche spécifique pour des raisons fonctionnelles ou purement visuelles. Il a ainsi été démontré que les flèches de poutre ne dépassant pas L/300 sont généralement acceptables. Cette valeur est souvent utilisée au moment du calcul à l’état limite de service. Il est néanmoins important d’analyser pourquoi un contrôle du déplacement a lieu, sur quel type de structure et pour quelles charges. Si, par exemple, la poutre est dotée d’une contre-flèche pour compenser la flèche induite par le poids propre, la limite de flèche ne s’applique qu’aux déplacements dus aux charges imposées.

Pour le calcul des poutres en vue du stockage et pour les charpentes de comble, les flèches admises sont généralement de l’ordre de L/200 à L/150. Le tableau 6.1 donne des exemples de valeurs limites dans différentes situations. Il ne s’agit cependant que d’exemples et il convient de considérer également la situation réelle et les limites de l’annexe nationale française.

Tableau 6.1 : Exemples de limites de flèche pour différentes combinaisons d’actions.

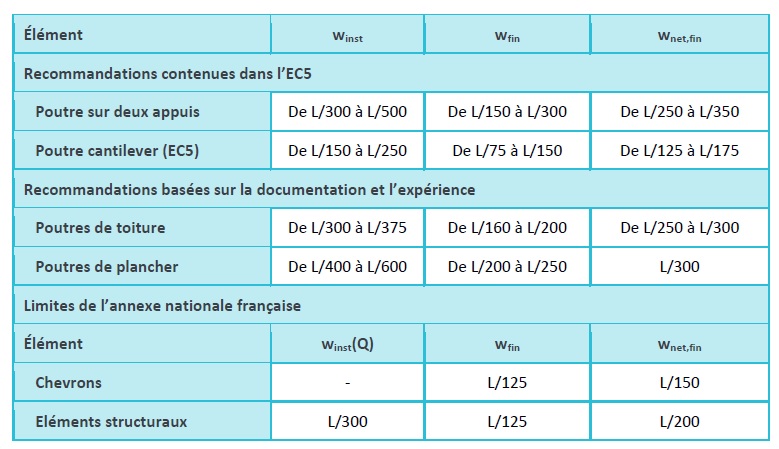
Au moment de déterminer la limite de flèche, il convient de tenir compte des éléments suivants :

la portée,
le type de structure et sa fonction,
le risque d’endommagement du plafond ou des matériaux de couverture,
les exigences esthétiques,
le nombre de fois où la flèche maximale est susceptible de se produire et sa durée,
l’évacuation des eaux du toit,
l’effet sur les éléments tels que les cloisons au-dessus ou en-dessous de l’emplacement de la flèche.

Dans toutes les situations, il est important de définir les problèmes liés aux flèches susceptibles de se poser, et s’ils risquent d’affecter l’aspect ou d’entraîner une détérioration. Les paragraphes ci-après donnent des exemples de combinaisons de valeurs limites, de combinaisons d’actions et de valeurs de calcul de la flèche :

Un mur non porteur situé sous une poutre déformée risque d’être endommagé si la flèche de la poutre est trop importante. Il convient de déterminer la valeur de l’espace libre requis entre la poutre et le mur et de l’utiliser comme limite. La valeur de calcul de la flèche peut être calculée selon la combinaison d’actions de l’équation 6.7. Cela peut être considéré comme un exemple de contrôle concernant l’endommagement permanent.
Lorsque le plancher d’un salon ne comporte aucun matériau sensible ni aucun risque d’endommagement des structures adjacentes, il peut faire l’objet d’un seul contrôle des charges à long terme. Les valeurs élevées des déformations sur une période plus courte ne poseront aucun problème. Dans ce cas, il est parfois suffisant de calculer les déformations selon une combinaison d’actions quasi-permanente, à savoir :

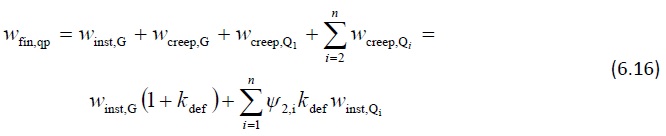
Dans certains cas, il est plus judicieux de contrôler uniquement les flèches à long terme, c’est-à-dire l’augmentation de la flèche au fil du temps, et de ne pas prendre en compte les flèches instantanées. Ceci est notamment le cas lorsqu’une poutre est dotée d’une contre-flèche suffisamment importante pour neutraliser l’effet instantané de la charge permanente. C’est également le cas lorsque le contrôle concerne l’aspect et l’utilité et non l’endommagement.
Lorsqu’il convient de contrôler les déformations liées aux réactions d’appui, le contrôle doit se baser sur une combinaison de charges de service. Étant donné que les déformations élastiques ne constituent dans la plupart des cas qu’une part mineure de la déformation, les niveaux de charges plus importants de courte durée n’affectent pas considérablement l’amplitude de la déformation. Les déformations dépendant dans une large mesure du comportement sur le long terme, il convient de baser le calcul sur une combinaison d’actions quasi-permanente. Il est également judicieux d’utiliser pour le coefficient k_def des valeurs plus importantes que celles utilisées dans les contrôles de la flèche, car le fluage perpendiculaire au fil est plus important que le fluage dans le sens du fil. Par ailleurs, il est parfois important dans ce cas d’estimer le retrait libre dans la partie comprimée.

6.2.5. Méthodes pour éviter les problèmes de déformation

Dans la pratique, il est impossible d’éviter les déformations lorsque le lamellé-collé est utilisé comme matériau de construction. Il est néanmoins possible, à l’aide de meilleurs outils de prévision, d’éviter les déformations d’une amplitude telle qu’elles risquent de poser problème. En plus de prévoir l’amplitude des déformations au cours de la durée de vie, il est intéressant de trouver des solutions conceptuelles garantissant des déformations moins importantes. Dans le cas des poutres, l’effet des variations d’humidité est fondamental. Cela signifie qu’il convient de prendre en compte les conditions climatiques liées au bâtiment dans lequel le bois est destiné à être utilisé. Il est également essentiel de déterminer si le climat varie selon les côtés de la structure en bois lamellé-collé. Cela est le cas des structures dotées d’un séparateur climatique. La variation du climat selon les côtés peut entraîner une augmentation des problèmes de déformation.

Lorsque les assemblages sont sollicités en compression, il est important d’éviter que la compression soit perpendiculaire au fil, car il s’agit de la direction la plus sensible en ce qui concerne la charge et les effets des variations d’humidité. L’utilisation de plusieurs types de matériaux dans un même bâtiment peut également être source de problème. Une poutre risque par exemple de s’incliner si l’une de ses extrémités est située sur un mur en béton et l’autre sur une structure en lamellé-collé. Dans ce cas, il convient d’insérer une pièce en bois entre le béton et la poutre afin que les deux extrémités subissent une déformation de même amplitude.

Une autre méthode pour éviter les effets négatifs des variations d’humidité sur les structures en bois lamellé-collé – et ainsi réduire les déformations – consiste à utiliser un revêtement pour empêcher la pénétration de l’humidité dans le lamellé-collé. Cette solution n’est cependant pas raisonnable dans la plupart des cas, car elle exige un travail considérable et revient cher. L’imprégnation constitue une autre méthode, mais qui n’est pas, elle non plus, très rationnelle.

Un moyen courant de réduire les effets négatifs de la déformation consiste à doter la poutre d’une contre-flèche au moment de sa fabrication en usine pour entraîner une déformation dans la direction opposée à la flèche induite par la charge. La valeur de la contre-flèche peut être calculée à partir de la flèche induite par la charge, comme cela a déjà été montré dans ce chapitre.

Il est en outre très important que l’ingénieur se penche sur la question suivante : quelle est la limite d’aptitude au service acceptable ? Souvent, le concepteur utilise à l’égard des valeurs limites des règles très simples, qui sont appropriées dans certains cas, mais trop générales dans d’autres.

6.2.6. Méthodes de calcul pour différents types de structures en bois lamellé-collé

Le calcul de la flèche est le même pour tous les types de structures en ce qui concerne les combinaisons d’actions (cf. Section 6.2.3). La présente section regroupe plusieurs équations à utiliser pour différents types d’éléments structuraux. Souvent, le meilleur moyen de déterminer la déformation d’une structure est d’utiliser la conception assistée par ordinateur, auquel cas il est important de se rappeler que les niveaux de charges ainsi que les propriétés des matériaux – c’est-à-dire les combinaisons d’actions et les valeurs moyennes des modules d’élasticité et de cisaillement – doivent être corrects.

6.2.6.1. Poutres droites à hauteur constante

Les équations nécessaires au calcul de la flèche des poutres droites à hauteur constante en fonction de la flexion sont indiquées sur la plupart des abaques.

Pour les poutres dont le rapport L/h est inférieur à 10, il est utile de déterminer les déformations de cisaillement en plus de la flexion. Il est possible de ne pas en tenir compte dans les autres cas.

Dans le cas d’une poutre en appui simple soumise à des charges uniformément réparties, la flèche à mi-portée est la suivante :

où l’indice b désigne la flexion. La flèche due au cisaillement est donnée dans ce cas par :

où l’indice s désigne la flèche due au cisaillement. Les valeurs moyennes des modules E et G doivent être utilisées.

Dans le cas des poutres continues, la flèche n’est généralement pas problématique. La flèche maximale intervient en principe aux travées d’extrémité.

6.2.6.2. Poutres droites dont la hauteur varie de façon linéaire

Le plus simple pour calculer les flèches des poutres à simple et à double décroissance est d’utiliser un ordinateur. (Les calculs manuels à l’aide d’équations de dimensionnement impliquent une quantité considérable de calculs.) Les flèches des poutres à simple décroissance en appui simple ou des poutres à double décroissance symétriques peuvent être estimées à l’aide de la formule suivante :

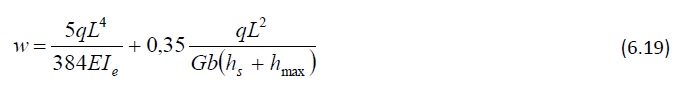
où

I_e = bh_e ³ /12

h_e = h_s + 0,33L·tan $alpha$ pour les poutres à double décroissance

h_e = h_s + 0,45L·tan $alpha$ pour les poutres à simple décroissance

h_max = h_ap pour les poutres à double décroissance et h_l pour les poutres à simple décroissance

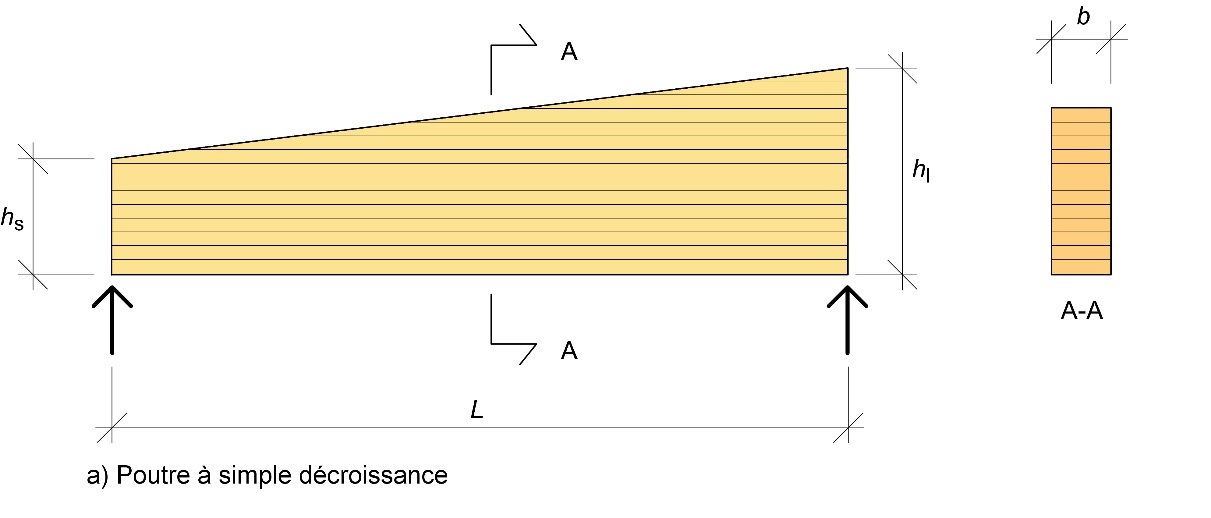
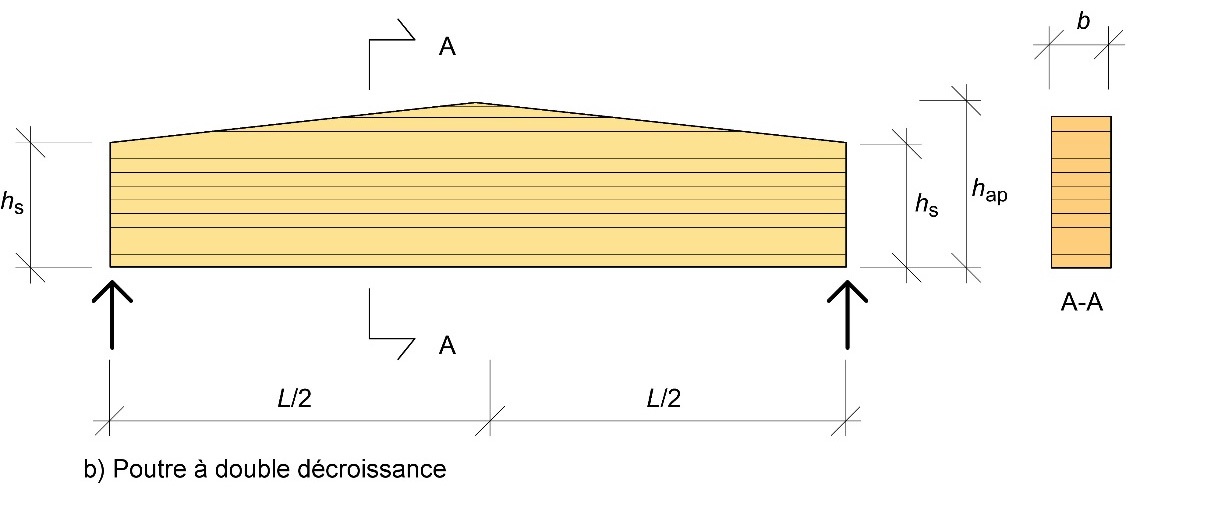
Figure 6.4 : Poutres à inertie variable

Lorsqu’une poutre se caractérise par 2L/(h_s+h_max) > 25, il est possible de ne pas prendre en compte le second terme de l’expression ci-dessous, qui correspond à la contribution de la déformation de cisaillement à la flèche.

Pour effectuer des calculs plus précis, les équations et les valeurs suivantes peuvent être utilisées (Porteous & Kermani, 2007).

Poutre à inertie variable soumise à une charge concentrée P à mi-travée

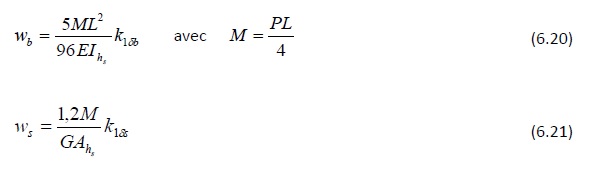
Poutre à inertie variable soumise à des charges uniformément réparties

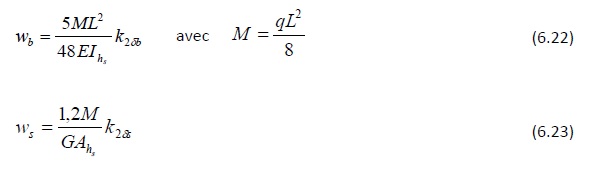
Poutre à double décroissance soumise à une charge concentrée

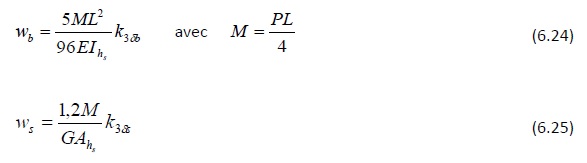
Poutre à double décroissance soumise à des charges uniformément réparties

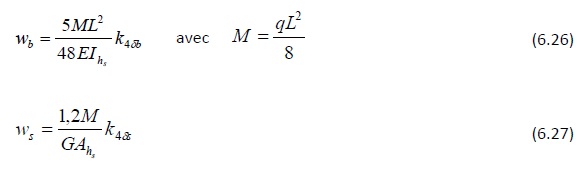
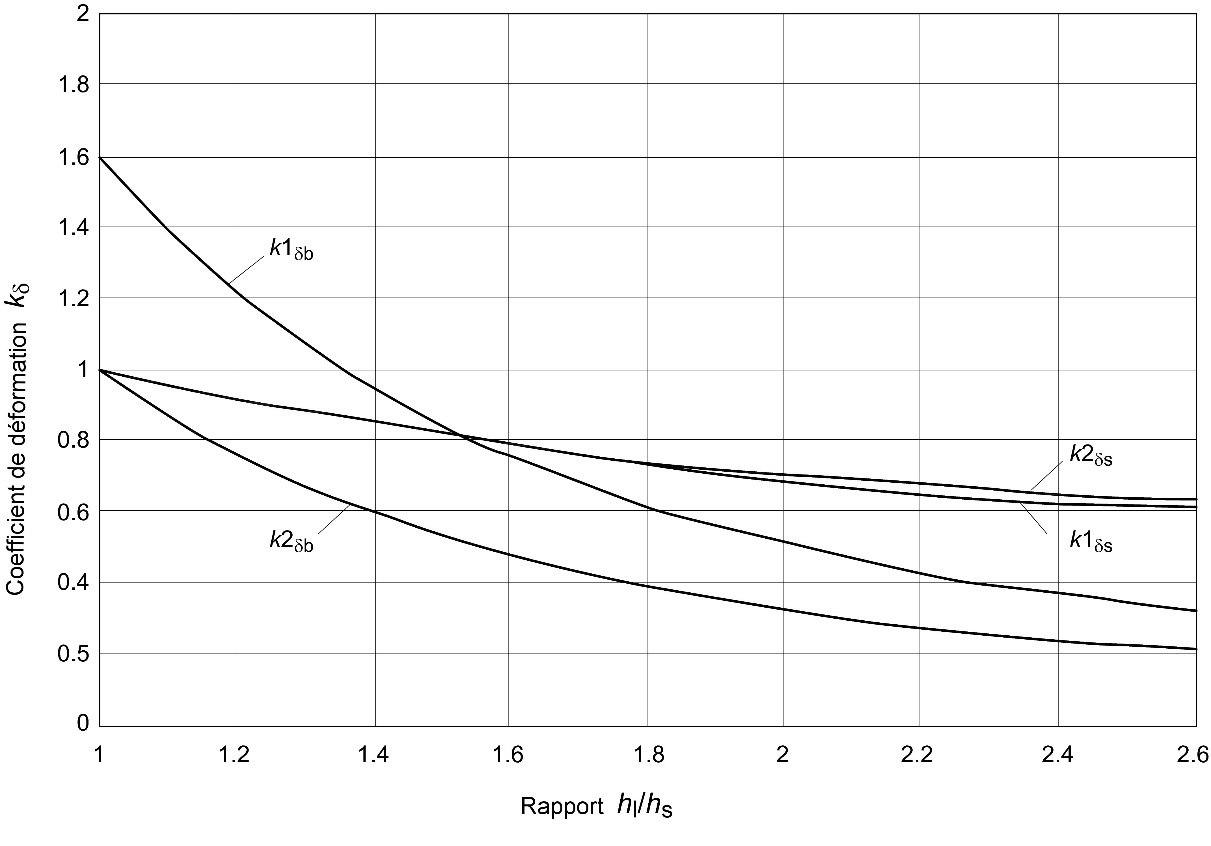
Figure 6.5 : Valeurs de k_δb et de k_δs pour les poutres à inertie variable.

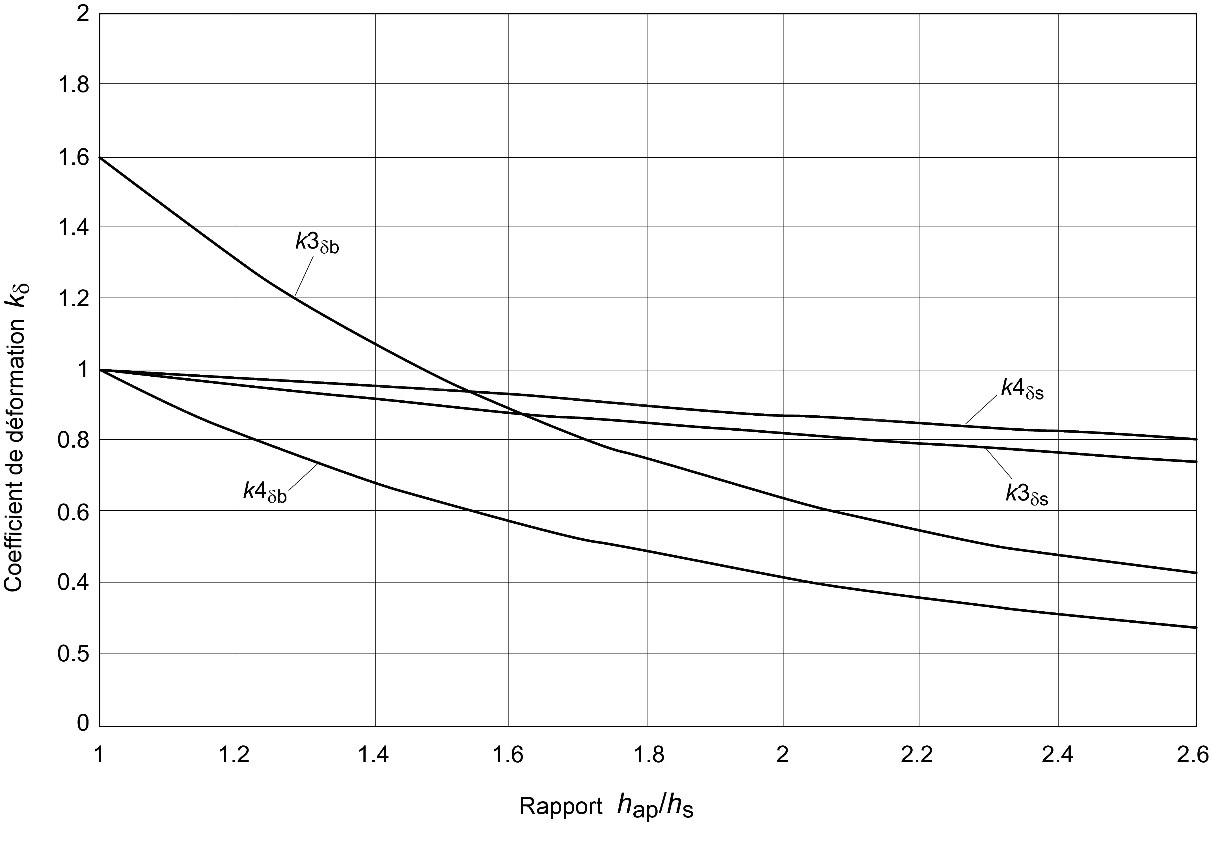
Figure 6.6 : Valeurs de k_δb et de k_δs pour les poutres à double décroissance.

6.2.6.3. Poutres courbes

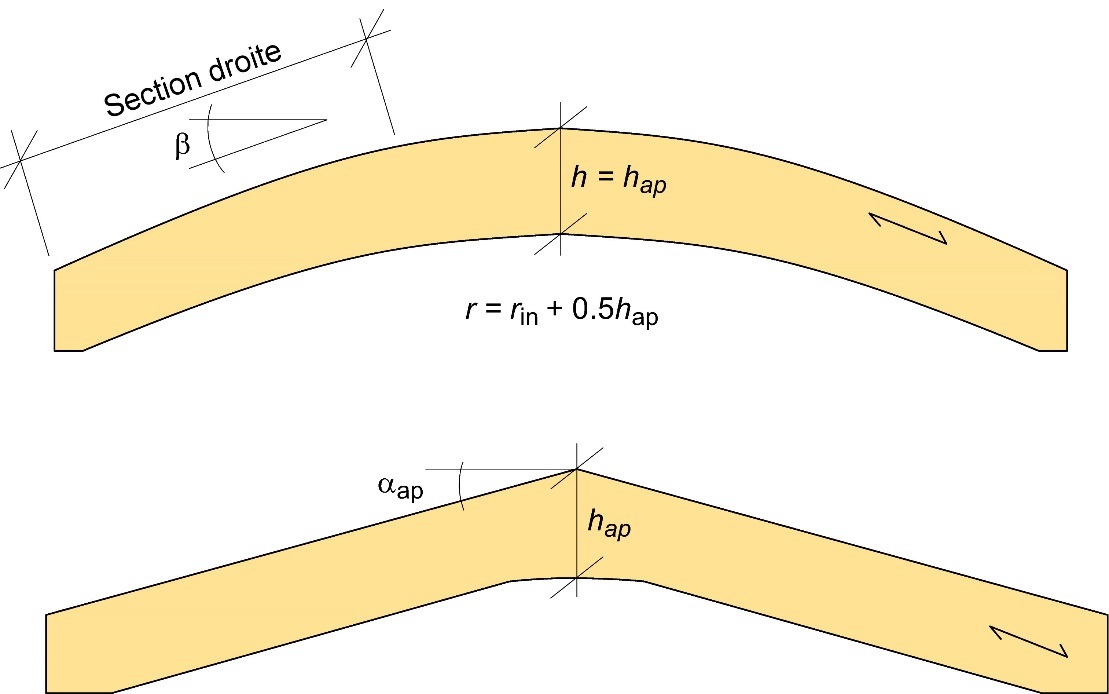
Figure 6.7 : Poutre courbe (figure du haut) et poutre banane (figure du bas).

Dans le cas des poutres courbes, le calcul des flèches est complexe, mais il est possible d’utiliser les équations suivantes pour obtenir une estimation des déplacements.

où w_q correspond à la flèche calculée pour une poutre à double décroissance symétrique avec une portée et une section transversale identiques à celles d’une poutre courbe au niveau des appuis et à mi-travée (cf. Chapitre 7).

Le déplacement horizontal au niveau de l’appui « libre » peut être estimé à l’aide de l’expression suivante :

où

f distance verticale entre la zone neutre au niveau de l’appui et le faîtage

h hauteur de la poutre au niveau de l’appui

L portée

w flèche verticale à mi-portée.

6.2.6.4. Poutres treillis

Il est plus difficile de calculer la flèche des poutres à treillis en bois lamellé-collé que des poutres simples, car les déformations sont aussi bien induites par les éléments lamellés collés que par les assemblages. Il est possible d’évaluer la flèche d’une poutre à treillis parallèle sans tenir compte des déformations dans les assemblages en calculant la flèche d’une poutre massive avec un moment de résistance :

où

Ai = aire de la section transversale des éléments externes

ai = distance entre la ligne d’épure des éléments externes et le centre de gravité de la poutre à treillis.

En raison des déplacements intervenant dans les assemblages, les déformations induites dans les poutres à treillis sont plus importantes que dans les poutres massives. Le problème est que l’augmentation de la flèche dépend du nombre d’assemblages dans la poutre ainsi que des types d’assemblages. Des mesures ont démontré que la flèche peut augmenter de 50 % maximum comparé à un cas où aucun déplacement n’intervient dans les assemblages.. Cette valeur correspond à une augmentation induite après un certain nombre d’années. Les assemblages réalisés par crampons sont les plus rigides ; ils entraînent des déformations moins importantes que ceux réalisés à l’aide de pointes et de panneaux de contreplaqué.

Il est donc recommandé de fabriquer les poutres à treillis avec une contre-flèche (aux membrures supérieure et inférieure) d’une amplitude d’environ L/150 quand L/h = 12 et L/200 quand L/h = 10. Le plus simple pour calculer les flèches des poutres à simple et à double décroissance est d’utiliser un logiciel.

6.2.6.5. Fermes à trois articulations

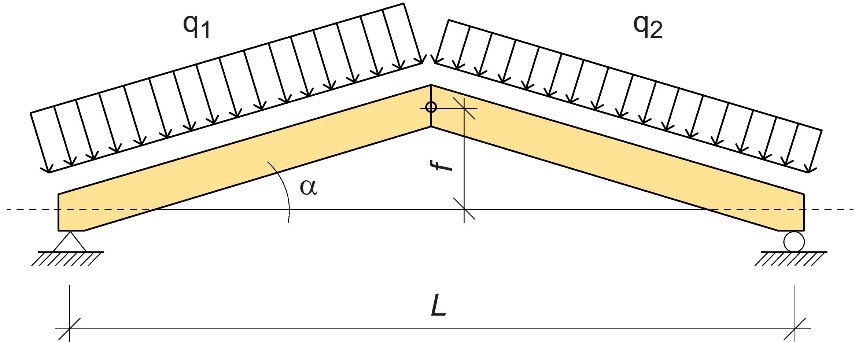
Figure 6.8 : Ferme à trois articulations avec des poutres de toiture simples et une barre tendue.

Sous des charges uniformément réparties vers le bas (comme illustré dans la Figure 6.9), la flèche verticale du faîtage peut être obtenue à l’aide de l’expression suivante :

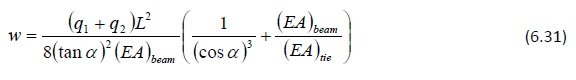
Si les appuis sont fixes, le second terme de l’expression entre parenthèses sera égal à 0.

6.3. VIBRATIONS

L’aptitude au service inclut le confort de l’usager lorsque la structure est soumise à des effets dynamiques, tels que les vibrations générées par des pas sur un plancher. Il s’agit d’une question complexe, car elle est liée à la masse du plancher et à la disposition des éléments structuraux dans le plancher, qui assurent une répartition latérale des charges dynamiques appliquées et un amortissement de la vibration produite.

Les usagers des bâtiments ou de tout ouvrage d’art ressentent les mouvements basse fréquence de trois façons :

les accélérations induisent des forces sur le corps qui sont ressenties par les organes de l’équilibre,
repères visuels (mouvement d’objets posés sur/suspendus à la structure par rapport à l’observateur, par exemple),
repères auditifs (craquement ou cliquetis dus aux mouvements de la structure, par exemple).

Les vibrations d’origine humaine qui se produisent dans les structures relèvent presque toujours d’un problème d’aptitude au service dans le sens où elles sont source de nuisance pour les usagers. Dans certains cas, la personne qui subit le mouvement en est aussi la cause, alors que dans d’autres, les nuisances sont provoquées par les activités d’autres individus. L’activité de la personne qui subit la vibration est donc importante. Lorsqu’une personne marche sur un plancher, elle tolère une amplitude de vibration beaucoup plus importante que lorsqu’elle est tranquillement assise pour se reposer, lire ou écrire. La catégorisation de la perception humaine et de la tolérance doit aussi bien refléter l’activité en cours que la relation entre la source et l’organe sensoriel. À cet égard, les définitions suivantes sont généralement utilisées :

La souplesse d’un plancher est associée à la sensation de flèche et de vibration du plancher autogénérées par un pas pendant le temps de contact du pied avec la surface du plancher.
Les perturbations vibratoires provoquées par des pas sur un plancher se caractérisent par une sensation de vibration du plancher induite par des personnes autres que la personne gênée.

En principe, la souplesse ne constitue un problème que si elle est associée à des planchers légers ou à des planchers souples sous une charge concentrée. Ce genre de plancher est courant dans les constructions en bois légères et dans d’autres types de bâtiments dotés de planchers traditionnels à solivage. Concernant la réponse de la structure de plancher, la souplesse inclut une élasticité statique et une vitesse impulsive alors que la perturbation vibratoire inclut une vitesse impulsive et une vibration stationnaire.

6.3.1. Charges dynamiques

En fonction des différentes sources de charges et contre-mesures applicables, les structures affectées par des vibrations d’origine humaine peuvent être regroupées ainsi :

immeubles résidentiels,
immeubles de bureaux,
bâtiments industriels,
ouvrages pour les piétons (passerelles, notamment dans les centres commerciaux),
gymnases et salles de sport,
salles de danse et de concert.

Il existe un nombre considérable de mouvements rythmiques corporels différents qui induisent diverses charges dynamiques. Les activités qui génèrent des mouvements rythmiques synchronisés (lorsque plusieurs personnes exercent une activité physique comme de la danse, par exemple) sont particulièrement problématiques. Le fait que plusieurs personnes agissent en synchronie pendant 20 secondes ou plus peut induire des charges approximativement périodiques qui provoquent une vibration structurale presque stationnaire.

Les forces provenant des déplacements humains dépendent de nombreux facteurs, et notamment des caractéristiques de la ou des personne(s) concernée(s), de l’activité en cours (marche, course, saut), du nombre de personnes, de l’éventuelle coordination des activités des différents individus et des caractéristiques de la surface du plancher. Les vibrations désagréables des planchers en lamellé-collé sont généralement associées aux forces produites par une personne marchant ou courant.

6.3.1.1. Réponse aux charges dynamiques

Du point de vue structural, un plancher en bois lamellé-collé peut être considéré comme une plaque mince bidimensionnelle renforcée par une série de poutres. En règle générale, ce système bidimensionnel est simplifié à la façon d’une structure à poutres unidimensionnelle en vue du calcul tenant compte de la surcharge et du poids propre spécifiés dans les précédentes sections. Dans la plupart des cas, les propriétés de rigidité statique des structures de plancher en bois lamellé-collé garantissent des performances satisfaisantes au regard de la vibration. Il est néanmoins arrivé que des structures de plancher – conçues pour satisfaire les critères de flèche habituels sous des charges uniformément réparties – révèlent des problèmes de vibration.

Les nouvelles méthodes de construction ont eu un impact considérable sur les caractéristiques vibratoires de certains planchers en lamellé-collé. Ces méthodes utilisent notamment des solives en bois d’ingénierie préfabriquées, des chapes de béton et des planchers flottants. La disponibilité de poutres à treillis et de solives en bois a permis des portées plus longues et des structures de plancher à travées multiples continues, alors que l’utilisation d’une chape de béton a considérablement modifié les propriétés massiques des planchers en lamellé-collé.

Il existe plusieurs méthodes de calcul concernant les problèmes de vibration et un certain nombre d’études ont été réalisées en vue d’améliorer ces méthodes.

6.3.1.2. Facteurs affectant la réponse humaine aux vibrations de plancher

Au moment d’analyser la réponse humaine aux vibrations transitoires dans une structure de plancher, les facteurs les plus importants sont notamment les composantes de fréquence, l’amplitude de la réponse et l’amortissement de la vibration.

6.3.1.3. Composantes de fréquence

Concernant les vibrations, les planchers sont généralement divisés en deux catégories : les planchers à basse fréquence et les planchers à haute fréquence. La fréquence fondamentale des planchers à basse fréquence est inférieure à 7-8 Hz, tandis que celle des planchers à haute fréquence est supérieure à 7-8 Hz. Les planchers à basse fréquence sont généralement des structures lourdes, telles que des planchers en béton. La catégorisation des planchers en planchers à basse ou à haute fréquence tire son origine des différentes réponses des types de planchers à la marche. Dans le cas des planchers à basse fréquence, les parties basse fréquence de la marche (les parties continues) sont les plus importantes, car elles entraînent une réponse du plancher à la résonance. Cela signifie que lorsqu’il reste immobile, un individu peut sentir cette vibration de résonance. Un plancher à haute fréquence est plus sensible aux parties impulsives de la marche. Dans ce cas, un individu immobile peut ressentir l’impact généré par un individu qui passe à côté de lui et le marcheur peut éprouver une sensation de souplesse.

La fréquence naturelle fondamentale f1 d’un système structural bi-directionnel, tel qu’un plancher en lamellé-collé, est principalement régi par la rigidité du système dans la direction longitudinale de la solive EI_x, l’unité de masse m et la portée L. L’espacement de deux fréquences naturelles adjacentes est contrôlé par le rapport entre la rigidité dans la direction transversale de la solive EI_y et EI_x.

6.3.1.4. Amortissement

L’amortissement est une propriété qui influence l’amplitude de vibration en cas de vibration forcée et le taux de décroissance de l’amplitude de vibration en cas de vibration libre. L’augmentation de l’amortissement entraîne une décroissance rapide de la vibration libre. L’amortissement des matériaux, généralement faible, varie selon le type de matériau de construction utilisé. Le principal élément intervenant dans l’amortissement est le frottement : les détails structuraux (la façon dont les éléments sont fixés, par exemple) et les conditions aux limites au niveau des appuis contribuent à l’amortissement par frottement.

Les conditions limites des éléments fléchis peuvent considérablement affecter l’amortissement. Il a été démontré que dans le cas des poutres lamellées-collées dont chaque extrémité est en appui simple et des poutres sur corbeaux, le coefficient d’amortissement associé au mode fondamental est d’environ 1 %. Lorsque ces éléments ont des extrémités encastrées, le coefficient d’amortissement atteint environ 8 %. Dans le cas des planchers traditionnels à solivage, les coefficients d’amortissement efficace varient entre 1 et 3 % en fonction des détails du plancher et du mode considéré. L’application de masses imposées (objets) sur la surface d’un plancher peut accroître de façon considérable l’amortissement, en particulier si la structure est légère ou de petite taille.

En raison de leur faible poids propre, les planchers en lamellé-collé ne se caractérisent généralement pas par un important amortissement inertiel. Les structures de grande taille, et notamment celles qui incluent une épaisse chape de béton ou qui soutiennent une importante masse imposée, peuvent cependant faire exception.

6.3.2. Approches de calcul pour limiter les vibrations dans les planchers en lamellé-collé

La recherche fondamentale visant à comprendre les facteurs qui affectent la réponse humaine aux vibrations des planchers a ouvert la voie au développement d’approches de calcul pour empêcher les vibrations. Deux exemples sont présentés dans cette section.

6.3.2.1. Limiter la flèche sous une charge concentrée

Il a été démontré qu’il est possible de déterminer la flèche statique sous une charge concentrée pour prévoir la réponse humaine à la vibration des planchers. Une méthode courante pour ce faire consiste à déterminer la flèche statique sous une charge concentrée de 1 kN au centre d’une poutre seule dans le modèle le plus simple ou pour une structure de plancher bi-directionnelle. Les limites de flèche utilisées dans ces modèles relativement simples diffèrent en fonction des réglementations ou des manuels, mais aussi de la portée et de l’objectif de la conception.

Cette approche peut être considérée comme permettant de modéliser l’effet d’un pas. La charge statique simulant l’effet de la force d’un pied correspond à 1 kN appliqué au centre du plancher, la flèche du plancher à ce point a ne devant pas dépasser une certaine valeur limite. La flèche sous une charge concentrée est donnée par :

où, dans ce cas, P = 1 kN. Si l’approche la plus simple est utilisée, l’équation 6.32 donne la valeur de la flèche avec la rigidité à la flexion EI d’une seule solive. Dans la plupart des cas, ce calcul aboutit néanmoins à une surestimation de la flèche, car la solive est seulement un élément d’une structure porteuse bi-directionnelle. Il est possible d’utiliser la rigidité dans les deux directions du plancher pour estimer l’amplitude de la flèche.

où k est un coefficient de répartition des charges qui peut être calculé à partir des expressions suivantes :

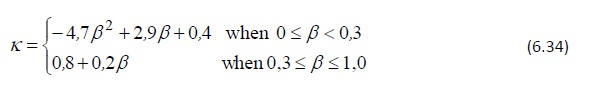
où (EI)_L correspond à la rigidité à la flexion du plancher selon l’axe fort, c’est-à-dire dans le sens longitudinal de la solive (Nm2 /m), (EI)_b correspond à la rigidité à la flexion du plancher dans la direction perpendiculaire à l’axe fort, c’est-à-dire dans le sens transversal de la solive (Nm2 /m), s correspond à l’espacement entre les solives et L correspond à la portée des solives.

6.3.2.2. Limiter la flèche sous une charge concentrée et la vitesse maximale causée par une impulsion unitaire

L’utilisation des paramètres de la réponse statique, telle que la flèche, au moment de réaliser un contrôle ne permet pas toujours d’obtenir des résultats satisfaisants. Les chercheurs sont conscients de cette limite et une recherche récente s’est davantage intéressée à l’étude des paramètres dynamiques. S. Ohlsson (1991) a été l’un des premiers à proposer des paramètres dynamiques dans le cadre de la conception. Dans le cas des planchers légers dont les fréquences naturelles sont supérieures à 8 Hz, deux paramètres doivent être vérifiés pour tenir compte des facteurs importants qui affectent la réponse humaine à la vibration des planchers :

1. Limite de flèche statique sous une charge de 1 kN au centre du plancher de 1,3±0,3 mm selon l’annexe nationale française pour un confort « standard »
2. Vitesse maximale v causée par une « impulsion unitaire de 1 Ns » < b^{[ f1ζ- 1]} (m/s)/Ns, où f₁ correspond à la fréquence naturelle fondamentale, ζ correspond à l’amortissement pour f₁ (en général 1 à 3%). Selon l’annexe nationale française, pour un confort « standard », 95≤b≤120.

Le premier critère est similaire à celui précédemment présenté et Ohlsson (1991) a précisé que ceci est un contrôle des composantes basse fréquence (< 8 Hz) de nature semi-statique. Le second critère est requis pour limiter l’amplitude de la réponse transitoire due à l’impact des talons d’un marcheur. La vitesse maximale, causée par une impulsion unitaire, pour une structure de plancher rectangulaire en appui simple sur les quatre côtés, valable pour f < 40 Hz, est calculée comme suit :

où n₄₀ représente le nombre de modes propres avec des fréquences propres inférieures à 40 Hz et est défini comme suit :

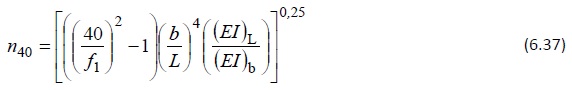
où b correspond à la largeur du plancher (m), L à la portée (m), m à la masse par unité de surface (kg/m² ), (EI)L à la rigidité (de plaque) à la flexion du plancher selon l’axe fort, c’està-dire dans le sens longitudinal des solives (Nm² /m), et (EI)b à la rigidité (de plaque) à la flexion du plancher dans la direction perpendiculaire à l’axe fort, c’est-à-dire dans le sens transversal des solives (Nm² /m).

Ohlsson a également établi une équation permettant de calculer la fréquence naturelle fondamentale d’un plancher :

Depuis sa présentation, cette méthode a été assez souvent utilisée et a généralement fourni des résultats satisfaisants, c’est-à-dire que les planchers conçus conformément à cette méthode ont révélé un comportement satisfaisant.

Dans le cadre du second critère précédemment mentionné, il convient de déterminer le coefficient d’amortissement ζ , ce qui n’est pas évident. Ohlsson indique que la valeur de ζ peut correspondre à 1 %, tout en précisant qu’il est possible de prendre en compte des valeurs supérieures.

Si les méthodes précédemment décrites fonctionnent bien dans certains cas, elles ne sont pas appropriées dans d’autres. Les méthodes de calcul ne donnent généralement qu’une valeur limite pour les planchers ; or bien souvent, le concepteur ne sait pas clairement ce qu’elle signifie. Dans quelle mesure les performances du plancher sont-elles améliorées lorsque la valeur limite est diminuée de 50 % ? Il est possible de trouver un certain nombre d’approches permettant de modéliser et de prévoir la réponse dynamique dans la documentation scientifique, mais toutes ces approches comportent des incertitudes et il est souvent difficile de trouver un modèle unique utilisable dans toutes les situations. Toutes les approches de calcul sont de nature semi-empirique et fournissent des solutions satisfaisantes pour le type de plancher sur lequel elles sont basées. Aucune ne fonctionne de façon pleinement satisfaisante lorsqu’elle est appliquée à d’autres types de plancher. Dans de nombreux cas, le meilleur moyen de connaître le comportement d’un plancher consiste encore à le tester.

6.3.3. Eviter les problèmes de vibration

Étant donné que les problèmes de vibration sont de nature complexe, il est difficile de donner une seule recommandation permettant de tous les résoudre. Une stratégie pratique consiste à essayer de concevoir des systèmes structuraux ayant des fréquences naturelles relativement élevées ; cette méthode est appelée « cibler une fréquence ». Elle suppose que les fréquences structurales les plus basses et les plus énergétiques des structures sont plus élevées que la fréquence d’excitation. L’objectif est d’éviter une coïncidence entre la sollicitation et les fréquences de réponse.

D’autres méthodes reposent sur un ajout de matériaux supplémentaires (pour augmenter la rigidité) ou une diminution de la portée. La tendance consiste cependant à diminuer la quantité de matériaux et à accroître la portée pour satisfaire d’autres objectifs du processus de conception. Il n’est donc pas surprenant que de plus en plus de problèmes de vibration dans les structures aient été constatés au cours des dernières années. Il est normalement plus facile d’accroître le rapport entre la résistance et le poids que d’accroître le rapport entre la rigidité et la masse des matériaux de construction.

Il existe bien entendu d’autres façons d’éviter les « planchers à problèmes ». Une approche potentiellement efficace consiste à accroître l’amortissement (ajout d’un amortissement artificiel ou installation d’amortisseurs harmoniques, par exemple), mais cette solution s’avère généralement complexe et/ou coûte cher. Il convient par ailleurs de faire attention aux détails, et notamment à la mise en place d’un blocage ou d’un contreventement en croix appropriés, et aux assemblages entre les différentes parties du système.

Les planchers flottants et les faux-planchers sont deux types de planchers particuliers. Ces types de superstructures sont de plus en plus utilisés en raison des exigences relatives à la protection contre les bruits d’impact et de la souplesse de montage des installations. La vibration ou les mouvements d’objets (cliquetis de verrerie ou mouvement de feuilles des plantes, par exemple) sont caractéristiques de ces types de planchers et il a été démontré que ces effets dépendent largement de la rigidité à la flexion du panneau de la surface supérieure. Lorsque les planchers flottants sont légers, des flèches locales apparaissent. Il est donc préférable de les limiter pour éviter ce problème. L’avantage des planchers flottants lorsque leur couche supérieure possède une rigidité suffisante à la flexion est qu’ils peuvent répartir efficacement les charges concentrées à différentes poutres de plancher, ce qui améliore la performance du plancher en matière de vibration.

Les flèches locales étant généralement difficiles à prévoir à partir de calculs d’ingénierie, il est recommandé de procéder à des essais pour les déterminer. La rigidité à la flexion de la couche supérieure des planchers flottants a un impact important sur les flèches locales.

Il est également essentiel de faire attention à la transmission des vibrations entre les différentes pièces par l’intermédiaire des poutres de plancher. Dans le cas de poutres continues, la vibration peut être transférée d’un appartement (ou d’une pièce) à l’autre et même si aucun problème n’est constaté dans la pièce d’où émane la vibration, il se peut que les voisins subissent une nuisance. Il a par ailleurs été démontré que les vibrations provenant d’un appartement voisin sont plus désagréables que celles dont la source réside dans l’appartement même.

6.4. RETRAIT/GONFLEMENT DU BOIS

La teneur en humidité des éléments lamellés-collés au moment de leur livraison est généralement de 12 %. Quelles que soient les conditions climatiques, la teneur en humidité s’ajuste avec le temps à la pression de vapeur relative environnante et à la température.

La teneur en humidité d’une structure varie sans cesse en raison des variations saisonnières. La variation est de 4 à 5 points d’humidité pour les éléments intérieurs et de 8 à 10 points d’humidité pour les éléments extérieurs. Lorsqu’il est à l’intérieur, le bois est généralement plus sec en hiver, alors que les structures extérieures sont plus sèches en été.

Comme tous les autres produits du bois, le lamellé-collé gonfle lorsque la teneur en humidité augmente et se rétracte lorsqu’elle diminue. Les jeux liés à l’humidité sont beaucoup plus importants dans le sens perpendiculaire au fil que dans le sens parallèle ; ils sont respectivement de 0,2 % et 0,01 % pour chaque pour cent de la variation de la teneur en humidité. Cela signifie qu’en cas de variations d’humidité normales, la variation dans le sens du fil (qui correspond généralement au sens longitudinal de la poutre) équivaut à environ 0,1 mm/m dans un milieu intérieur et à 0,2 mm/m dans un milieu extérieur. Dans le sens perpendiculaire au fil, les variations sont de 10 mm/m (à l’intérieur) et de 20 mm/m.

Lorsque le jeu perpendiculaire au fil est limité par des contraintes internes ou externes, il se peut que la résistance à la traction perpendiculaire au fil soit dépassée, ce qui provoque un écrasement ou un éclatement du bois. Les éléments de fixation et les assemblages doivent donc être conçus de façon à ce que le jeu normal lié à l’humidité soit le moins limité possible. À noter également que la rigidité et la capacité résistante des assemblages boulonnés peuvent être altérées s’ils ne sont pas correctement ajustés. Il convient si possible de resserrer ne serait-ce que les assemblages boulonnés fondamentaux lorsque le bois a séché.

Les variations de longueur sont en principe si faibles qu’elles ne doivent pas forcément être prises en compte, sauf dans les structures de très grande taille. Lorsque la teneur en humidité est répartie de façon inégale le long de la section transversale des éléments (poutres et poteaux dans une couche d’isolation, par exemple), ces derniers peuvent subir une déformation considérable due à la différence des jeux liés à l’humidité sur les côtés froid et chaud. Pendant l’hiver, l’un des côtés est dans un environnement chaud et sec alors que l’autre est en contact avec l’air extérieur, qui se caractérise par une teneur en humidité élevée. Le côté extérieur gonfle et devient plus long que le côté intérieur, ce qui explique pourquoi les toitures et les murs extérieurs ont tendance à se courber vers l’extérieur pendant l’hiver. En cas d’appui articulé et de jeu lié à l’humidité non contenu, la flexion vers l’extérieur peut être calculée à l’aide de la formule suivante :

où

L portée

∆L différence de longueur entre la face extérieure et la face intérieure en raisin d’un gonflement ou d’un retrait

h hauteur de l’élément.

Il est également important de faire attention aux effets des jeux liés à l’humidité dans les assemblages et lorsque des tirants sont utilisés pour transférer les charges, car les jeux liés à l’humidité peuvent entraîner une diminution de la capacité à transférer les forces entre les différents éléments structuraux. Il est parfois nécessaire de vérifier les assemblages ou les tirants et de resserrer les assemblages au cours de la durée de vie de la structure.