Les poutres lamellées-collées sont généralement de forme courbe et/ou à inertie variable. Elles permettent de répondre à certaines exigences architecturales, notamment d’obtenir une toiture inclinée, d’augmenter au maximum l’espace intérieur et de réduire les hauteurs d’appui requises au niveau des extrémités. Les types les plus couramment utilisés sont la poutre à simple décroissance, la poutre courbe à section constante, la poutre à double décroissance et la poutre banane (cf. Figure 7.1).
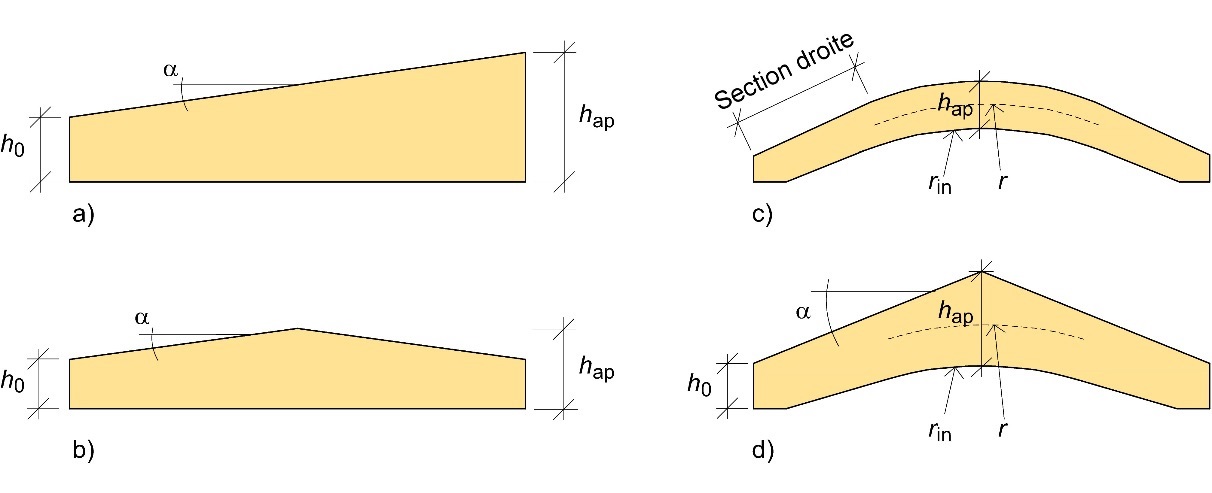
Figure 7.1 : Poutres lamellées-collées spécifiques : (a) simple décroissance ; (b) double décroissance ; (c) courbe ; (d) banane.
Tous ces éléments en bois présentent une spécificité : la distribution des contraintes de flexion n'est pas linéaire, d'où la nécessité d'en calculer les valeurs selon la théorie des plaques anisotropes. Toutefois, aux fins de calcul, il est possible de déterminer la contrainte de flexion maximale et les contraintes de cisaillement selon une approximation satisfaisante en s'appuyant sur la théorie des poutres simples pour les matériaux isotropes.
7.1. POUTRES A INERTIE VARIABLE
Les éléments de construction en bois, particulièrement ceux en lamellé-collé, sont généralement conçus avec une section transversale à hauteur variable (par ex. poutres à simple et à double décroissance, poutres continues présentant une section plus haute au niveau des appuis intermédiaires, etc.). En règle générale, cette section variable est obtenue en diminuant progressivement la hauteur des lamelles le long d'une rive. Dans la mesure où l'approche conceptuelle des poutres à simple décroissance et celle des poutres à double décroissance sont similaires, nous aborderons simplement dans cette section les poutres à double décroissance. Ce type de poutres offre une économie de matériau satisfaisante, étant donné que le tracé de la hauteur suit la courbe du diagramme des moments de flexion.
Les contraintes de flexion des poutres à inertie variable présentent une distribution non linéaire. De plus, sur ce type de poutres, la contrainte de cisaillement maximale ne se situe généralement pas au niveau de l'axe neutre, mais plutôt rapprochée du bord en décroissance (cf. Figure 7.2). Cette contrainte maximale intervient au niveau de l'axe neutre uniquement à l'appui d'une poutre en appui simple ou à l'extrémité libre d'une poutre cantilever. À noter que les contraintes de flexion et de cisaillement illustrées à la Figure 7.2 s’étendent parallèlement aux lamelles, et non parallèlement au côté incliné.
Dans la mesure où le moment et la hauteur varient tous deux le long de l'axe de la poutre, la contrainte de flexion maximale n’agit pas là où le moment est le plus important, mais à une section plus proche des appuis (cf. Figure 7.2).
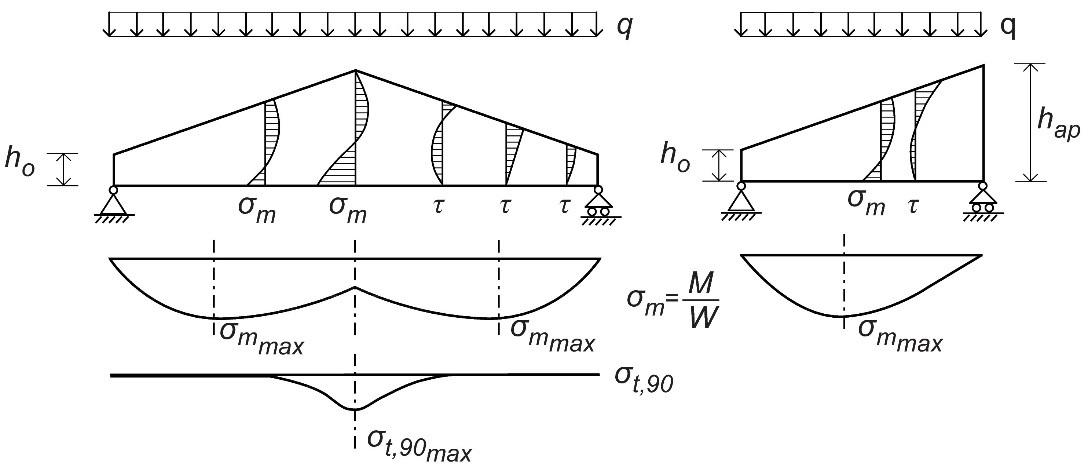
Figure 7.2 : Contraintes de flexion (σm), contraintes de cisaillement (σ) et contraintes de traction perpendiculaires au fil (σt,90)
sur une poutre à double décroissance (à gauche) et sur une poutre à simple décroissance (à droite).
Lorsque, comme dans la majeure partie des cas, le bord incliné présente une pente faible (à savoir α≤ 10° ), la décroissance influe très peu sur la distribution des contraintes de flexion. Aux fins de calcul, par conséquent, la contrainte de flexion maximale peut être déterminée de la même manière que pour une poutre à hauteur constante (soit σm = M/W), aussi bien au bord en décroissance qu'au bord droit. Cependant, la valeur de la résistance à la flexion fm doit être réduite au niveau du bord en décroissance, afin de tenir compte de l'effet de la contrainte de cisaillement et de la contrainte perpendiculaire au fil, lesquelles agissent simultanément avec la contrainte de flexion au bord en décroissance (cf. Figure 7.3). L'Eurocode 5 recommande de réduire la résistance à la flexion du bord en décroissance selon un coefficient kmα (cf. Section 7.3.1.).
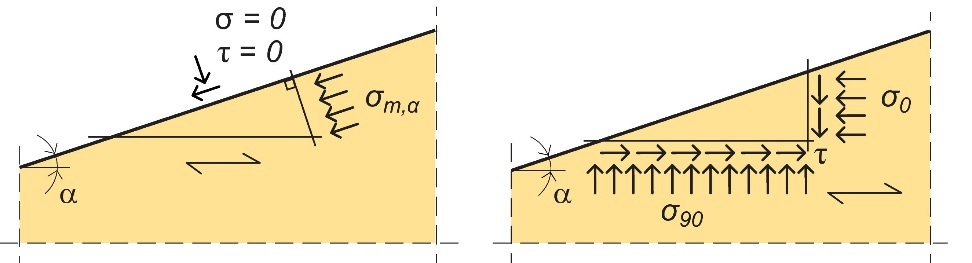
Figure 7.3 : Contraintes au niveau du bord en décroissance d'une poutre. À gauche : contrainte de flexion parallèle au bord
en décroissance σm,a (contrainte principale). À droite : contrainte de flexion σ0 parallèle au fil.
Il est possible de montrer que l'amplitude des contraintes perpendiculaires au fil (σ90) augmente au fur et à mesure que la pente du bord incliné augmente. Si le bord incliné se trouve sur le côté comprimé de la poutre, une compression perpendiculaire au fil (σc90) intervient lors de la flexion de la poutre. En revanche, si le bord incliné se trouve sur le côté tendu de la poutre (poutres à inertie variable retournées - cf. Figure 7.4), une contrainte de traction perpendiculaire au fil (σt90) se produit.

Figure 7.4 : À gauche : compression perpendiculaire au fil au niveau du bord incliné. À droite : traction perpendiculaire au fil au niveau du bord incliné (poutre retournée).
C'est pourquoi la pente du bord en décroissance devra être limitée. L'angle d'inclinaison 
Si la face supérieure d'un toit doit être linéaire (pente simple), en guise d'alternative aux poutres à inertie variable retournées, il est recommandé d'utiliser des poutres en ventre de poisson, lesquelles comprennent des lamelles continues sur le côté tendu et des lamelles inclinées sur le côté comprimé (cf. Figure 7.5). Cette solution permet de supprimer les contraintes de traction perpendiculaires au fil – aux effets néfastes.
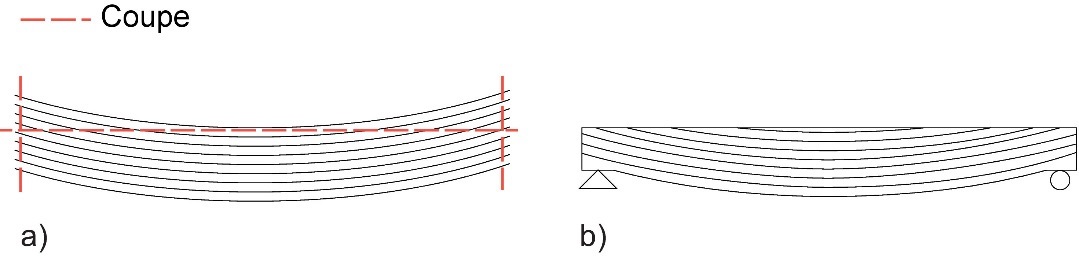
Figure 7.5 : À gauche : collage des lamelles. À droite : poutre en ventre de poisson.
7.2. POUTRES COURBES ET BANANES
Parmi les principaux avantages du bois lamellé-collé, on retrouve la possibilité de concevoir des éléments de construction courbes. Lors du process de fabrication, chaque lamelle est pliée selon la forme souhaitée avant que la colle ne sèche. D'un point de vue du comportement structural, il est important de faire une nette distinction entre les arcs et les poutres courbes. La différence fondamentale entre ces deux types de structures réside dans le fait que pour les arcs, aucun des deux appuis ne peut bouger (en d'autres termes, une poussée horizontale, et donc un effort normal, peuvent se produire), tandis que dans le cas des poutres courbes, l'un des appuis peut se déplacer librement le long de l'axe longitudinal de la poutre. Les arcs seront abordés au Chapitre 11. Afin d'éviter d'endommager les lamelles lorsque ces dernières sont cintrées, il convient de limiter la courbure. Des lamelles plus épaisses ne pourront pas être autant cintrées que des lamelles plus fines. Cette limitation de la courbure est également requise, afin de garantir l’absence de toutes contraintes de flexion résiduelles majeures dans l'élément fini. Il est possible de ne pas tenir compte de ces contraintes initiales dans le calcul. Cependant, si le rapport rayon de courbure(r)/épaisseur des lamelles (t) est trop faible, la résistance à la flexion de la poutre sera impactée par les contraintes de flexion résiduelles ; il conviendra alors de la réduire. Selon l'Eurocode 5, un tel facteur de réduction doit être appliqué pour r/t<240. En pratique, cependant, le rapport rayon de courbure/épaisseur des lamelles ne devra en aucun cas être inférieur à environ 170. Il convient de souligner le fait que les poutres courbes et bananes sont des éléments qui travaillent principalement en flexion (contrairement aux arcs qui travaillent essentiellement par force axiale). Il est donc important que l'un des deux appuis de la poutre puisse permettre des déplacements horizontaux dans le sens horizontal, parallèlement à la portée, sans générer d'autres forces dans la poutre.
Lorsqu'un moment de flexion est appliqué à une poutre initialement cintrée dans le plan de cintrage, outre des contraintes de flexion, des contraintes radiales (de traction ou de compression) interviennent également (cf. Figure 7.6). Si le moment appliqué tend à augmenter la courbure de l'élément lamellé-collé, les lamelles sont pressées plus fermement ensemble (Figure 7.6, à gauche) ; d'où des contraintes radiales de compression entre les lamelles. En revanche, si le moment de flexion appliqué tend à décintrer l'élément lamellé-collé, les lamelles s'écartent (Figure 7.6, à droite) ; d'où des contraintes radiales de traction entre les lamelles. Les contraintes radiales de traction devront être les plus faibles possible, dans la mesure où ces dernières peuvent provoquer une fissuration de l'élément.
Afin de réduire ce risque de fissuration et de rupture lié à la traction perpendiculaire au fil, les poutres courbes et bananes sont généralement renforcées au moyen de goujons collés, de vis autotaraudeuses ou de panneaux contreplaqués collés aux surfaces. La conception des éléments de renforcement est décrite à la Section 7.4.2.
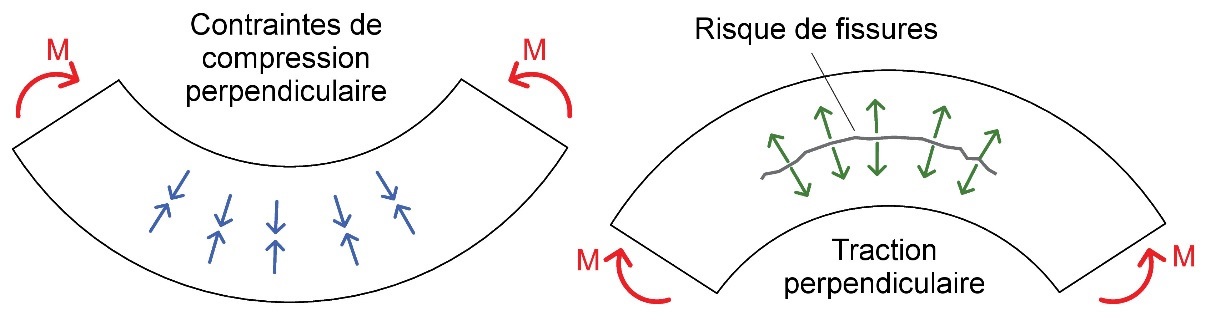
Figure 7.6 : À gauche : moment de flexion qui tend à accroître la courbure de l'élément lamellé-collé. À droite : moment de flexion qui tend à décintrer l'élément lamellé-collé.
La Figure 7.7 montre la zone d'apex d'une poutre courbe soumise à un moment de flexion constant. Supposons, dans un souci de simplification, une répartition linéaire des contraintes de flexion au niveau de la zone d'apex. Les forces résultantes de traction et de compression (T et C, respectivement) généreront clairement une force T90 dans le sens radial.
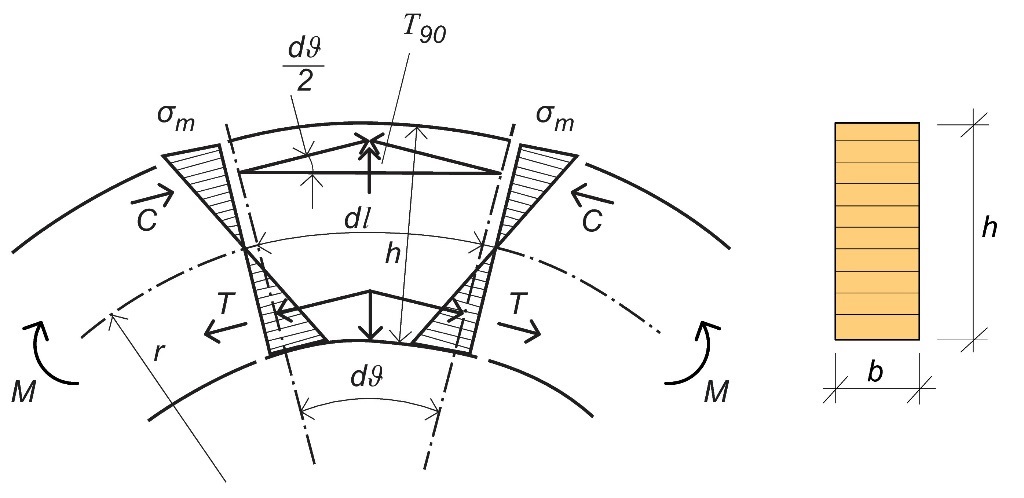
Figure 7.7 : Modèle simplifié de détermination des contraintes perpendiculaires au fil à l'apex d'une poutre courbe soumise à un moment de flexion pure positif.
Il peut être démontré que la contrainte de traction perpendiculaire au fil, induite par T90 (cf. Figure 7.7), est égale à :

L'Éq. 7.1 montre que la valeur approximative de la contrainte de traction perpendiculaire au fil σt,90 à l'apex d'une poutre courbe peut être obtenue en modifiant la contrainte de flexion parallèle au fil (σm =M/W) en appliquant un coefficient de forme kp=h/(4·r). Point important : le rayon de courbure r devra être suffisamment grand, de manière à réduire l'amplitude de la contrainte perpendiculaire au fil. En général, il est conseillé de choisir systématiquement un rayon r ≥ 5 m.
Selon différentes études, la résistance à la traction perpendiculaire au fil ft,90 dépend largement du volume de l’élément en bois contraint. La valeur de calcul de base de la résistance à la traction perpendiculaire au fil doit donc être modifiée. L'Eurocode 5 préconise de multiplier cette résistance ft,90 par un coefficient de modification kvol (<1).
Dans les cas où la contrainte de traction de calcul σt,90 dépasse la résistance à la traction définie par l'EC5 pour des contraintes perpendiculaires au fil, des organes d'assemblage mécaniques tels que des goujons collés ou des vis entièrement filetées peuvent être utilisés à des fins de renforcement (cf. Section 7.4).
7.3. METHODES DE CALCUL
Lors de la fabrication de poutres à inertie variable et bananes, il est généralement recommandé de placer les lamelles continues sur le côté tendu de la poutre, c'est-à-dire sur son côté inférieur, si la poutre est en appui simple et soumise principalement à des charges de gravité. Les lamelles en décroissance seront alors situées sur le côté comprimé de la poutre.
7.3.1. Poutres à inertie variable
En principe, la portée maximale de ce type de poutres est limitée à 30 m, principalement pour des raisons de contraintes de fabrication et d'économie de frais de transport. La pente ne devra en aucun cas dépasser 10°. Dans la pratique, une telle pente se situe dans une plage 1/20-1/10, à savoir 
Très souvent, les poutres à inertie variables sont fabriquées avec une contre-flèche, dont l'amplitude doit correspondre plus ou moins à celle de la flèche maximale sous charges permanentes, à laquelle il faut rajouter la moitié de la valeur de la charge variable principale (par ex. charge de neige).
En ce qui concerne les poutres symétriques en appui simple avec une charge uniformément répartie, la résistance à la flexion de l'apex (c’est-à-dire à mi-travée) n'atteindra jamais une valeur critique. La section transversale présentant la contrainte de flexion maximale se situe plutôt à une distance x0 de l'appui. Il est possible de déterminer analytiquement la position de cette section comme étant celle où la dérivée de la contrainte de flexion en fonction de x vaut zéro. On obtient alors le résultat suivant :

où h0 désigne la hauteur de poutre au niveau de l'appui, hap désigne la hauteur de poutre à l'apex et l désigne la portée. En ce qui concerne les géométries de poutres usuelles, la position de la contrainte de flexion maximale correspond approximativement à un quart de la portée (x0 ≈ l/4).
Pour des pentes 

où :
Md correspond au moment de flexion de calcul dans la section x=x0 ;
Wx0 correspond au module de résistance à la section transversale x=x0.
Très souvent, le lamellé-collé panaché est utilisé pour la fabrication de poutres à inertie variable ; c’est le cas, par exemple, du GL30C, un lamellé-collé consistant en des lamelles T22 et T15 dans les parties externe et centrale de la section transversale, respectivement. Pour ce type de poutres, la contrainte de compression maximale induite par le moment de flexion, à une distance x0 de l'appui, se produit en général au niveau des lamelles présentant la classe de résistance inférieure (à savoir T15). En théorie, la résistance de la poutre devrait être réduite par rapport à celle d'une poutre similaire comprenant une section transversale homogène et des lamelles de classe T22. Cependant, cette réduction de résistance n'est pas prise en compte, dans la mesure où ce défaut se produit quasi systématiquement au côté tendu de la poutre, là où se trouvent les lamelles à haute résistance (à savoir T22).
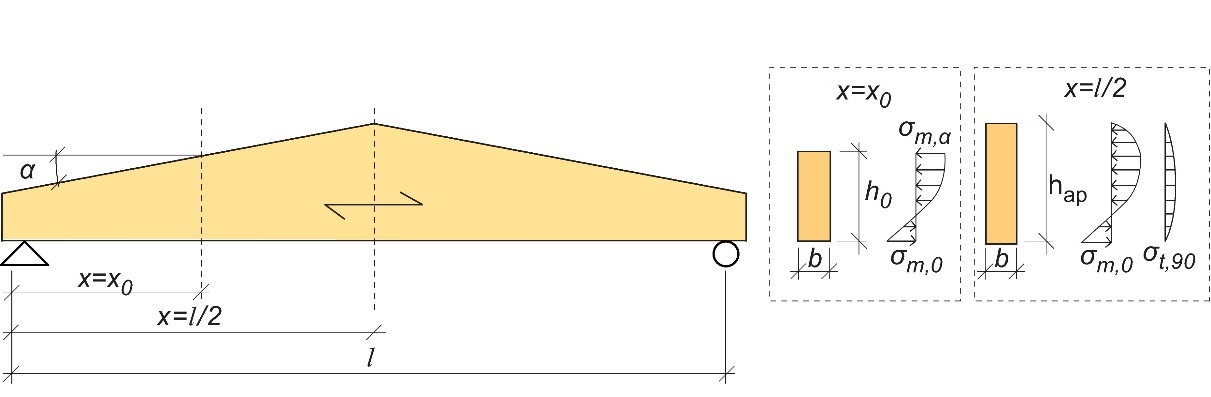
Figure 7.8 : Poutre à simple décroissance avec répartition réelle et non linéaire des contraintes de flexion et perpendiculaires
au fil à x=x0 et à mi-travée.
Au niveau de la fibre la plus à l'extérieur du bord en décroissance, les contraintes devront satisfaire l’expression suivante :

où :
σm,a,d et σm,0,d correspondent aux contraintes de flexion de calcul à un angle par rapport au fil et au bord droit, respectivement ;
fm,d correspond à la résistance de calcul à la flexion ;
km,
Selon l'Eurocode 5, le coefficient de réduction km,

où :
fv,d, ft,90,d et fc,90,d correspondent aux résistances de calcul définies par l'EC5 pour le cisaillement, la traction perpendiculaire au fil et la compression perpendiculaire au fil, respectivement.
Les valeurs de km,


où l désigne la portée de la poutre et R désigne le rayon de courbure des lamelles (généralement R > 100 m).
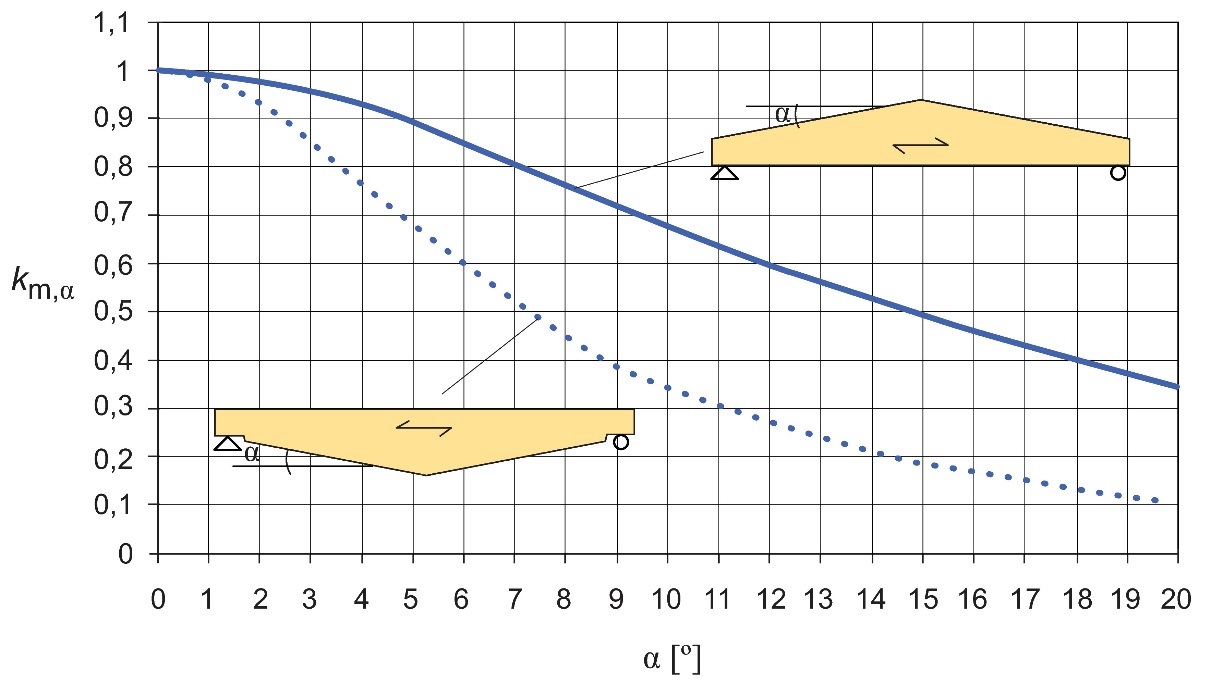
Figure 7.9 : Valeurs de km,a selon l'Eurocode 5 en fonction de différentes pentes du bord en décroissance ; lamellé-collé
GL30c. Classe de service 1 ; durée de la charge : moyen terme.
La valeur de calcul de la contrainte de traction perpendiculaire au fil sous moment de flexion peut être déterminée comme suit :

où :
Map,d correspond au moment de calcul à l'apex ;
Wap correspond au module de résistance de la poutre à l'apex ;
(0,2·tan 

La résistance à la traction perpendiculaire au fil doit alors être réduite, de manière à prendre en compte l'effet de volume. Selon l'Eurocode 5, il convient de satisfaire l'inégalité suivante :
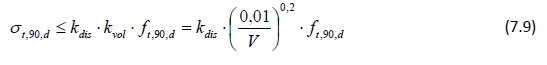
où :
ft,90,d correspond à la résistance de calcul à la traction perpendiculaire au fil ; kdis correspond à un coefficient qui permet de prendre en compte l'effet de la répartition des contraintes dans la zone d'apex. Il est possible de reprendre les valeurs kdis et V définies au Tableau 7.1 pour des poutres soumises à une charge uniformément répartie.
Tableau 7.1 : Valeurs de kdis et de V selon l'Eurocode 5 pour des types de poutres courantes (« b » correspond à la largeur de la poutre).
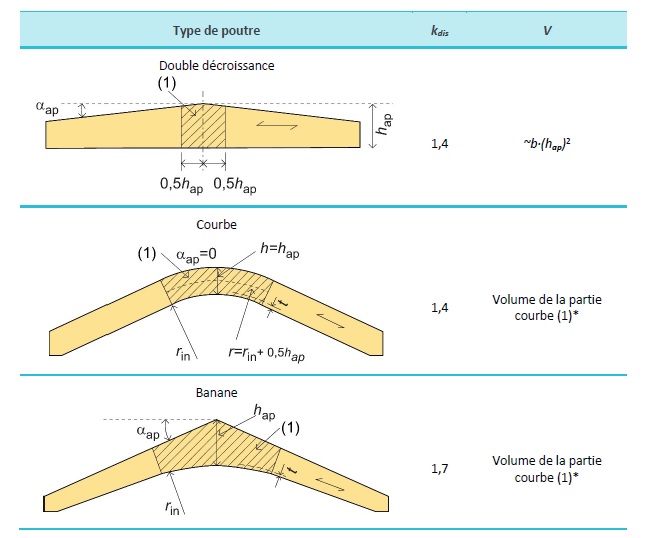
* La valeur V ne doit pas, cependant, dépasser 2/3Vb, où Vb est le volume total de la poutre.
En général, le calcul final des poutres à inertie variable inclura les vérifications suivantes :
- Résistance à la flexion à une distance x0 de l'appui ;
- Résistance au cisaillement et force portante de l'appui ;
- Résistance à la traction perpendiculaire au fil à l'apex ;
- Déversement (cette vérification porte généralement sur une partie isolée de la poutre entre deux pannes adjacentes).
7.3.2. Calcul préliminaire de poutres à double décroissance en appui simple soumises à une charge uniformément répartie
Cette section propose des indications générales concernant le calcul préliminaire d'une poutre à double décroissance en appui simple. Une structure typique de cette poutre est présentée à la Figure 7.10, conjointement avec les principaux paramètres géométriques.
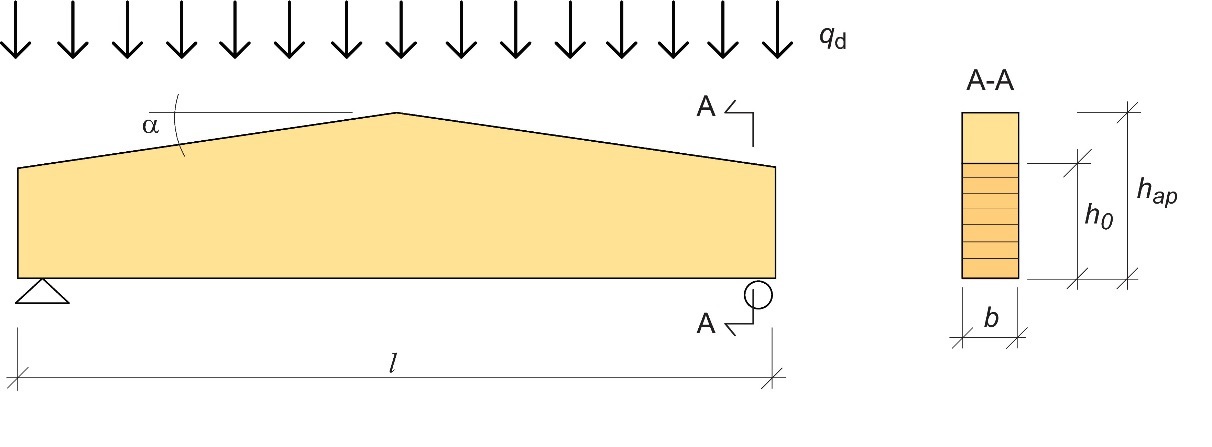
Figure 7.10 : Poutre lamellée-collée à double décroissance typique
Lors de l'étape préliminaire de dimensionnement, les variables détaillées ci-après sont généralement connues :
- Intensité de la charge de calcul qd
- Pente du toit
(généralement comprise dans la plage 2o -6o )
- Portée l généralement ≤ 30 m)
Toutes les valeurs de calcul de résistance du matériau sont également connues, dans la mesure où elles dépendent de la classe de résistance du lamellé-collé choisi.
Le calcul préliminaire permettra d'estimer les dimensions des sections transversales au niveau de l'appui et de l'apex.
7.3.2.1. Largeur de poutre
Afin de réduire les problèmes d'instabilité latérale, particulièrement au moment du montage, la poutre devra présenter une largeur correspondant à au moins 1/7 de la hauteur de la poutre qui, elle-même, correspondra à environ 1/20 - 1/15 de la portée de la poutre. Ce qui donne :

7.3.2.2. Hauteurs de poutre
La résistance de la poutre dépend en règle générale de sa résistance à la flexion au niveau de la section transversale située à une distance x0 de l'appui (cf. section 7.1). Cependant, le paramètre x0 est déterminé à partir de la hauteur de poutre aussi bien au niveau de l'appui qu'à l'apex ; des valeurs qui sont a priori inconnues. Lors du calcul préliminaire, il est donc supposé que x0 est situé à l/4 de l'appui, et que la résistance à la flexion de la poutre fm,d à x0 est quelque peu réduite du fait de la décroissance du bord supérieur. Un coefficient de réduction associé à la décroissance avec 


7.3.3. Poutres courbes et bananes
La portée maximale des poutres courbes et bananes ne devra pas dépasser 20 m, principalement du fait de la limitation imposée par les contraintes de traction perpendiculaires au fil qui agissent dans la zone d'apex. Par ailleurs, afin de réduire le risque de rupture liée à la traction perpendiculaire au fil, la pente de ces poutres devra, de préférence, être inférieure à 15° (s’agissant des poutres courbes, cette pente correspond à celle des éléments linéaires). La hauteur au niveau de l'appui devra être égale à au moins l/30 pour les deux types de poutres. La hauteur à l'apex est en principe comprise entre l/20 et l/15 pour les poutres courbes, et entre l/15 et l/10 pour les poutres bananes. La largeur ne devra pas être inférieure à un septième de la hauteur de la poutre à l'apex (b ≥ hap/7). Le rayon de courbure r (cf. Figure 7.11) choisi est généralement supérieur à 10 m.
Les flèches verticales de ces poutres ne jouent pas un rôle important. Néanmoins, les déplacements horizontaux au niveau des appuis peuvent être relativement amples. C'est pourquoi il convient de s'assurer que ces déplacements n'impliquent aucun effort latéral imprévu sur les structures porteuses (en principe murs, poteaux).
La section transversale présentant la contrainte de flexion maximale est située à une distance x0 de l'appui. Il est possible de déterminer la position de cette section à l'aide de l'Éq. 7.2. Le calcul des poutres courbes et bananes tient compte, cependant, des contraintes de traction perpendiculaires au fil, lesquelles sont principalement induites par les charges de gravité, et par les variations d'humidité du bois. Ces contraintes sont plus importantes dans la zone d'apex de la poutre (zone (1) sur la Figure 7.11).
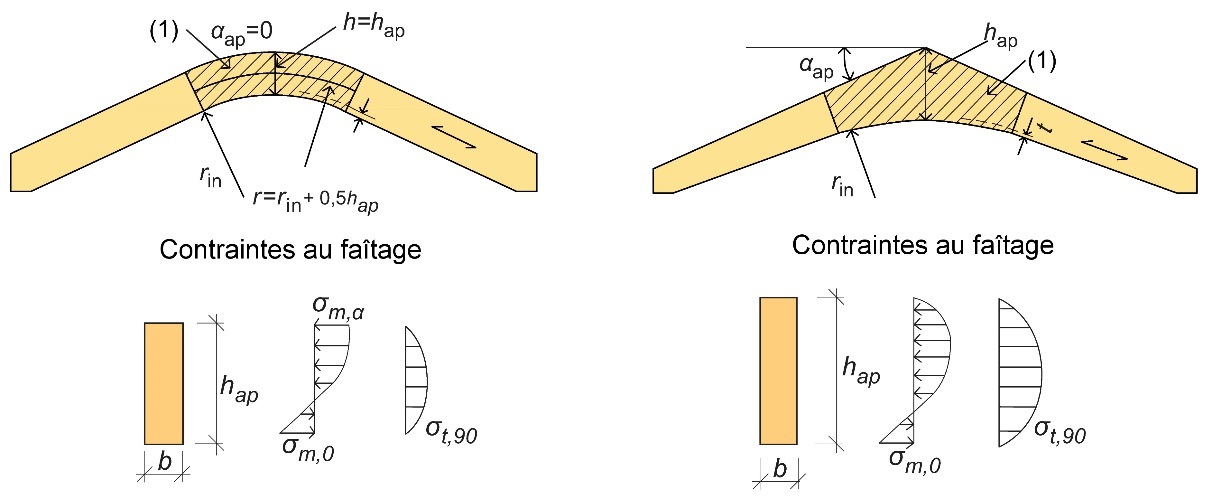
Figure 7.11 : Contraintes de flexion σm,0 et contraintes de traction perpendiculaires au fil σt,90 : poutre courbe (à gauche) et
poutre banane (à droite).
Selon l'Eurocode 5, la valeur de calcul de la contrainte de traction perpendiculaire au fil induite par le moment de flexion de calcul à l'apex (Map,d) peut être obtenue comme suit (cf. symboles de la Figure 7.11) :
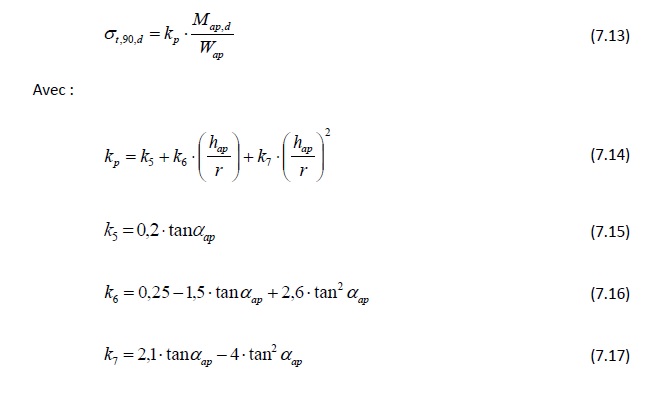
kp correspond à un coefficient obtenu au moyen de l’analyse par éléments finis, défini comme le rapport entre la valeur de calcul de la contrainte perpendiculaire au fil et la contrainte de flexion admissible à la zone d'apex. La Figure 7.12 montre la variation de kp en fonction de hap/r. D'autres courbes sont représentées pour différents angles d'apex αap. Le matériau utilisé est un lamellé-collé GL30c.
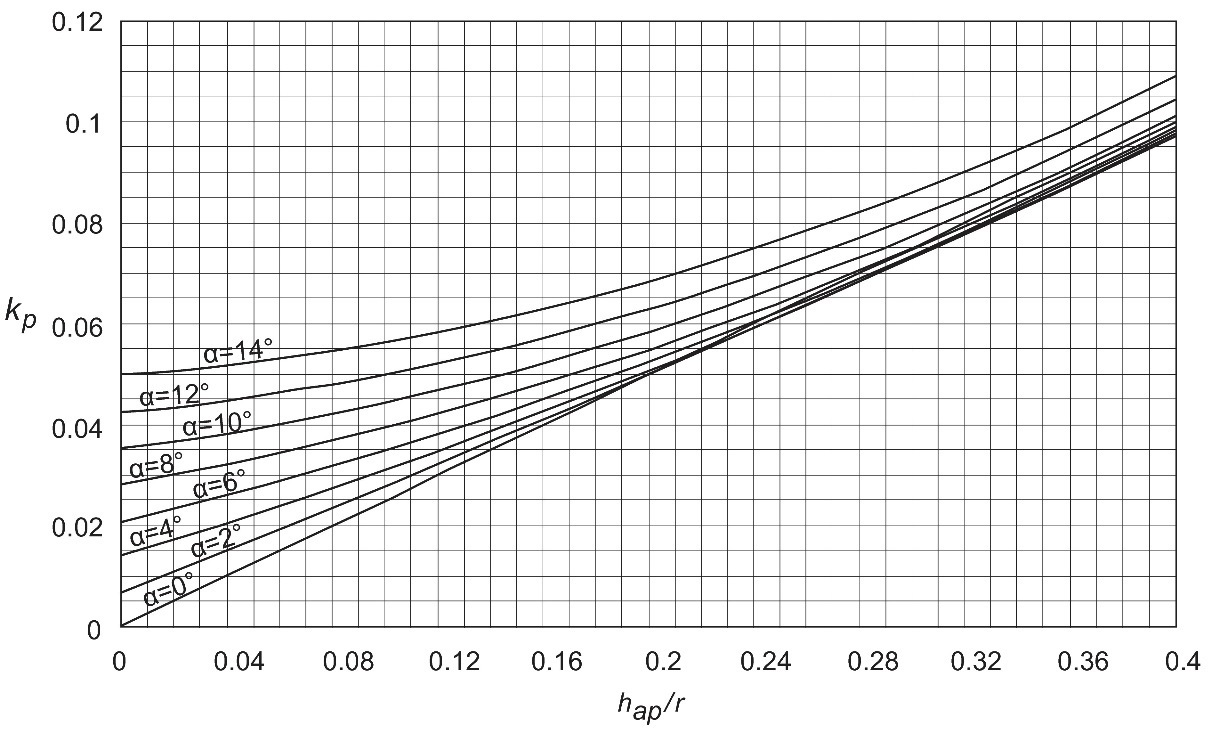
Figure 7.12 : Coefficient kp selon l'Eurocode 5 pour différentes valeurs de hap/r ; lamellé-collé GL30c.
La résistance perpendiculaire au fil doit être vérifiée de la même manière que pour les poutres à inertie variable (cf. Éq. 7.9).
La résistance à la flexion à l'apex peut parfois constituer le paramètre déterminant associé à des poutres courbes présentant un grand rayon de courbure ; mais très rarement celui des poutres bananes. Selon l'Eurocode 5, la contrainte de traction induite par le moment de flexion de calcul à l'apex (Map,d) peut être calculée comme suit :
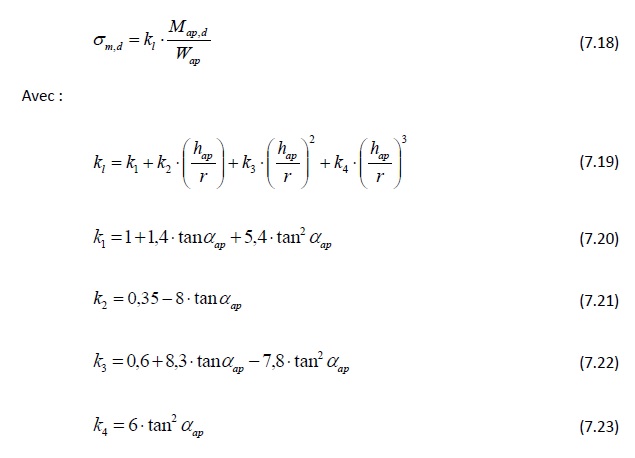
kl correspond à un coefficient obtenu au moyen de l’analyse par éléments finis qui tient compte de la géométrie de la poutre. La Figure 7.13 montre la variation de kl en fonction de hap/r. D'autres courbes sont représentées pour différents angles d'apex αap.
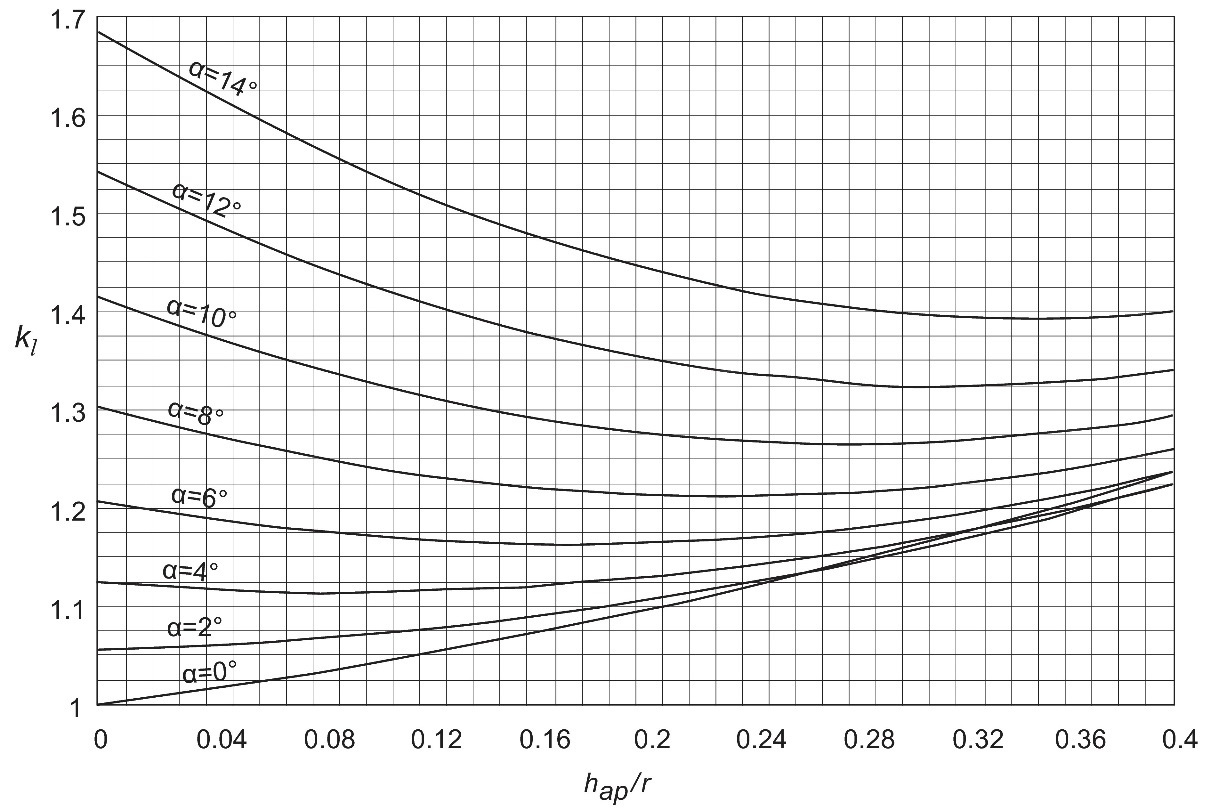
Figure 7.13 : Coefficient kl selon l'Eurocode 5 en fonction de différentes valeurs de hap/r ; lamellé-collé GL30c.
La résistance à la flexion des lamelles courbes doit être réduite en fonction des contraintes résiduelles induites par le cintrage des lamelles lors de la fabrication de l'élément structural. Il suffit alors de multiplier la valeur de base de la résistance à la flexion fm,d par un coefficient de réduction kr.

La valeur de kr diminue à mesure que le rapport rin/t (cf. Tableau 7.2) baisse.
Tableau 7.2 : Coefficient de réduction de la résistance à la flexion kr selon l'Eurocode 5 en fonction du rapport rin/t, où rin correspond au rayon de courbure et où t correspond à l'épaisseur des lamelles.

En principe, le calcul final des poutres courbes et bananes inclura les vérifications suivantes :
- Résistance à la flexion à une distance x0 de l'appui, pour les poutres bananes et les poutres courbes à hauteur variable (dans certains cas, il conviendra également de vérifier la contrainte de flexion à l'apex) ;
- Résistance au cisaillement et force portante à l'appui ;
- Résistance à la traction perpendiculaire au fil à l'apex ;
- Déversement (cette vérification porte généralement sur une partie isolée de la poutre entre deux pannes adjacentes. Dans le cas de poutres courbes, cette partie peut être considérée comme un élément linéaire).
7.3.4. Calcul préliminaire de poutres courbes et bananes en appui simple soumises à une charge uniformément répartie
Cette section propose des indications générales concernant le calcul préliminaire (prédimensionnement) de poutres courbes et bananes en appui simple. Certains paramètres géométriques utiles pour le calcul de ces types de poutres sont présentés au tableau 7.3.
Tableau 7.3 : Paramètres géométriques pour le calcul préliminaire de poutres courbes et bananes.
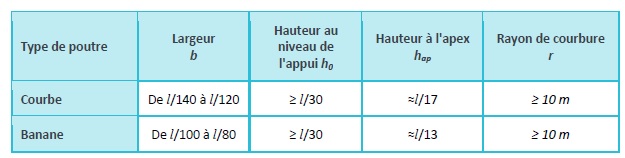
Comme dans le cas des poutres à inertie variable, la charge de calcul qd, la pente du toit α et la portée l sont en principe des paramètres connus.
La première étape consiste à déterminer la hauteur de la poutre au niveau de la contrainte de flexion maximale, c'est-à-dire à x= x0 de l'appui. Comme pour les poutres à inertie variable, il est donc supposé que x0 est situé à l/4 de l'appui, et que la résistance à la flexion de la poutre fm,d devra être réduite selon un coefficient km,α≈0,9. Sur la base de ces hypothèses, il est possible d'estimer la hauteur de poutre requise à x= x0 à l'aide de l'équation suivante :

Les hauteurs de poutre au niveau de l'appui et à l'apex peuvent alors être calculées en fonction des relations géométriques liant les différents paramètres de la Figure 7-14.
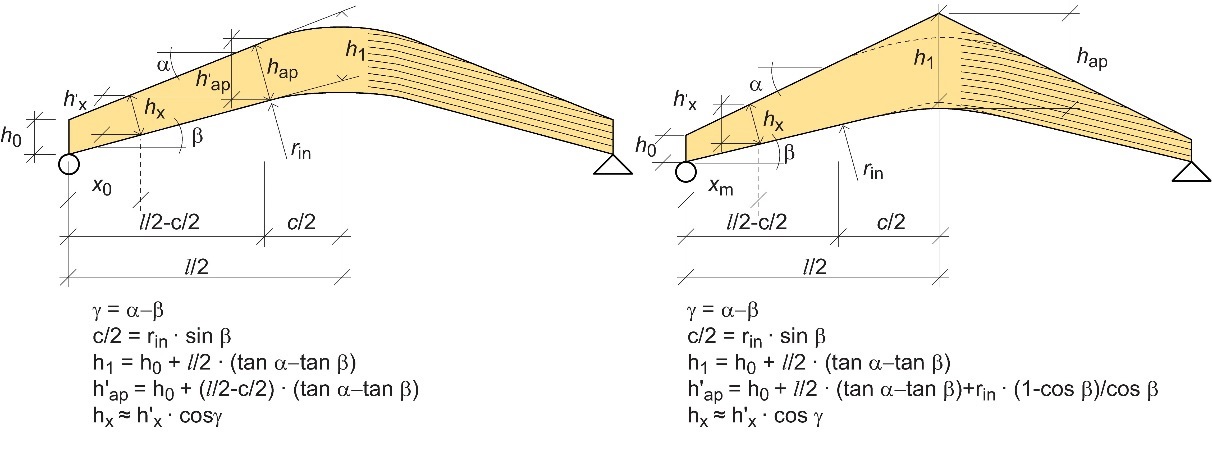
Figure 7.14 : Relations géométriques associés aux poutres courbes (à gauche) et aux poutres bananes (à droite).
7.4. RENFORCEMENT DES POUTRES A DOUBLE DECROISSANCE, COURBES ET BANANES SOUMISES A DES CONTRAINTES DE TRACTION PERPENDICULAIRES AU FIL
Nous avons vu dans les sections précédentes les équations permettant de calculer les contraintes de traction perpendiculaires au fil dans les zones d'apex de poutres (i) courbes, (ii) bananes ou (iii) à double décroissance selon l'Eurocode 5. Parmi ces trois types de poutres, les poutres bananes sont les plus sujettes à fissuration du fait de contraintes perpendiculaires au fil dans la zone d'apex. Une première tentative pour réduire l'impact négatif de ces contraintes consiste à rendre la partie supérieure de l'apex « mobile ». Dans la pratique, il s'agit de relier la partie supérieure de la poutre à la partie au-dessous de la poutre uniquement au moyen d’assembleurs mécaniques tels que des vis (cf. Figure 7.15). De cette manière, le comportement statique de la poutre banane sera pratiquement identique à celui d'une poutre courbe similaire ; d'où des contraintes de tractions perpendiculaires au fil moins importantes.
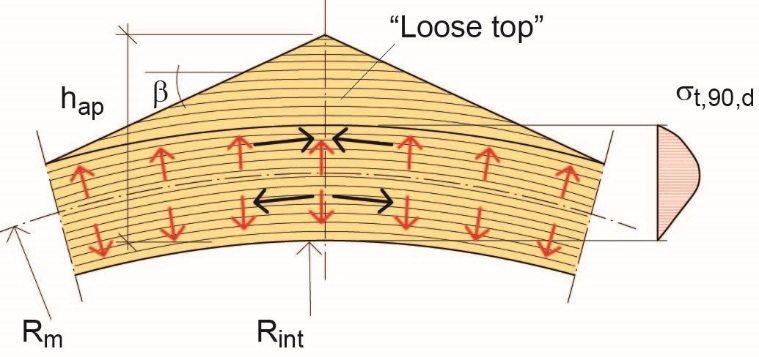
Figure 7.15 : Poutre banane dont la partie supérieure est rendue mobile pour réduire les contraintes de traction perpendiculaires au fil.
Plus la distance depuis la section transversale de l'apex augmente, plus les contraintes de traction perpendiculaires au fil diminuent, suivant la forme de la poutre et la répartition des charges. La Figure 7.16 montre une répartition typique de ces contraintes dans une poutre banane soumise à des charges uniformément réparties.
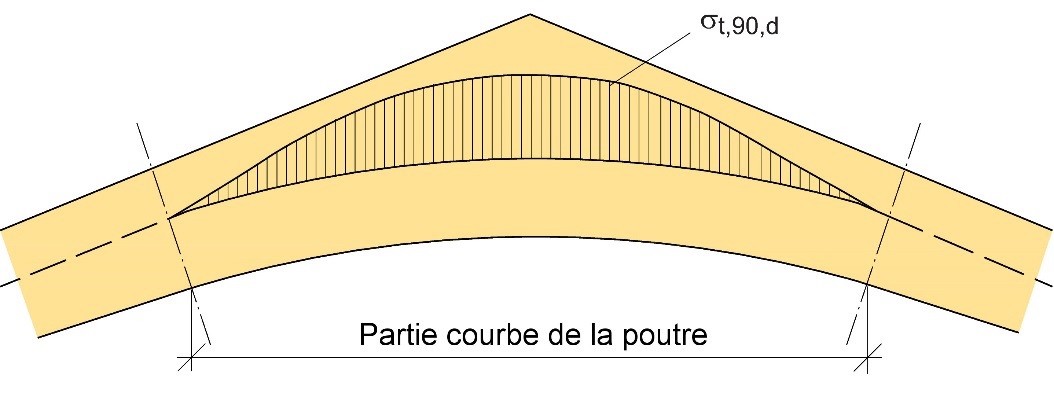
Figure 7.16 : Répartition typique des contraintes de traction perpendiculaires au fil dans une poutre banane.
7.4.1. Méthodes courantes de renforcement de structures soumises à une traction perpendiculaire au fil aux effets néfastes
En règle générale, le renforcement des poutres courbes, bananes ou à double décroissance est de deux types :
- Renforcement interne ;
- Renforcement externe.
La méthode de renforcement interne implique l'utilisation des éléments suivants :
- Goujons filetés collés ;
- Barres d'armature crénelées en béton collées ;
- Vis filetées.
La Figure 7.17 présente plusieurs configurations typiques d’éléments de renforcement internes.
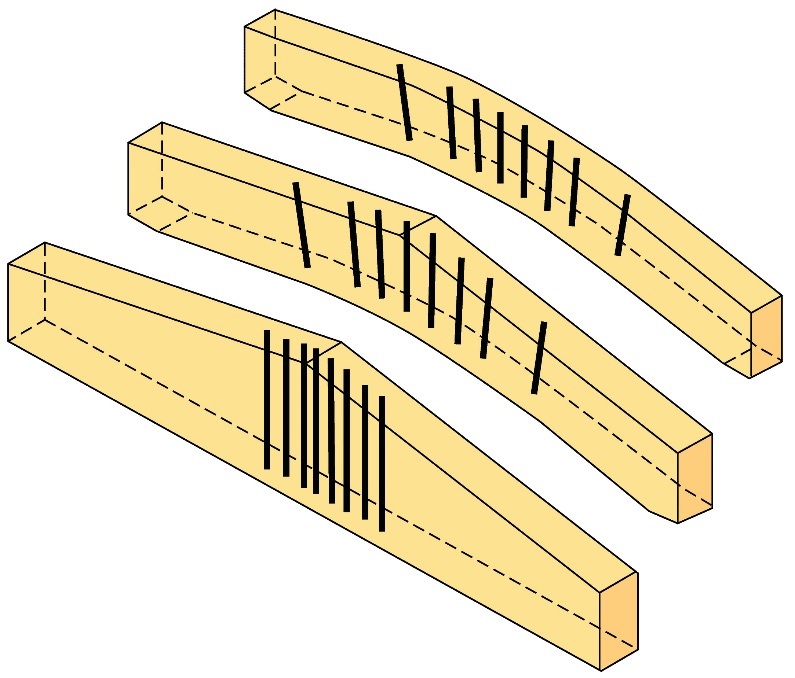
Figure 7.17 : Configurations typiques d’éléments de renforcement internes de poutres lamellées-collées soumises à une traction perpendiculaire au fil.
Dans les cas où la méthode de renforcement interne est adoptée, il conviendra de prendre en compte la réduction de la section transversale du fait de la présence de barres ou de vis au moment de vérifier la résistance à la traction perpendiculaire au fil.
La méthode de renforcement externe implique l'utilisation des éléments suivants :
- Bois contreplaqué ou lamibois collé ;
- Plaques collées dont le fil est perpendiculaire à celui de la poutre ;
- Connecteurs à plaque métallique emboutie.
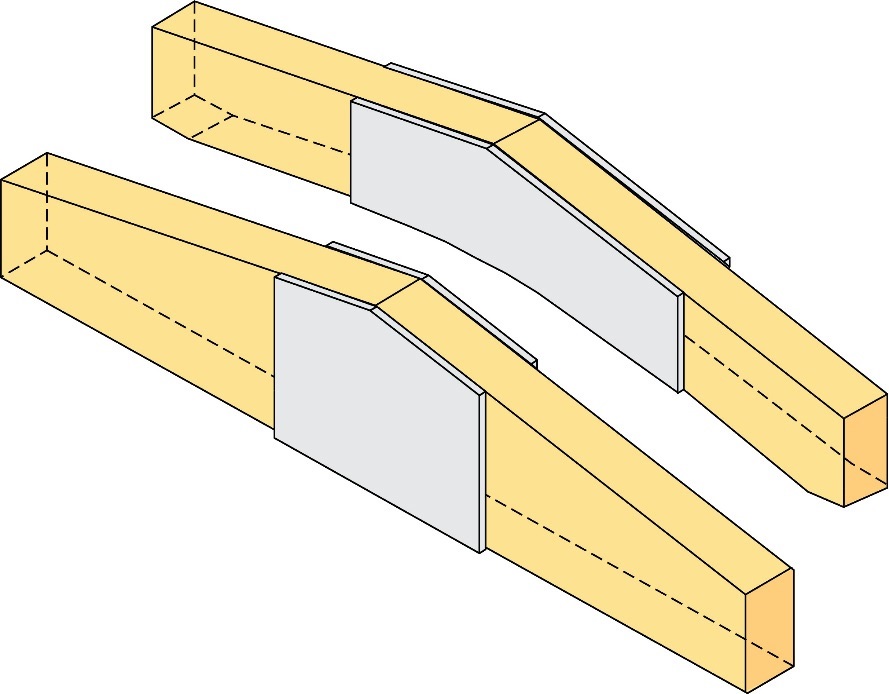
Figure 7.18 : Configurations typiques d’éléments de renforcement externe de poutres lamellées-collées soumises à une traction perpendiculaire au fil.
La section suivante aborde simplement le calcul d’éléments de renforcement internes, dans la mesure où celui d’éléments de renforcement externe peut être envisagé de façon similaire.
7.4.2. Calcul du renforcement
Un élément de renforcement devra être prévu dans les zones de la poutre présentant une traction perpendiculaire au fil significative, principalement là où les contraintes calculées dépasseront les valeurs de résistance correspondantes. En général, le renforcement appliqué s'apparente à celui illustré à la Figure 7.19.
Les poutres bananes et courbes sont fabriquées de manière à inclure des éléments linéaires à leurs extrémités et une courbure dans leurs éléments centraux. Dans le cas de ces poutres, les contraintes de traction interviennent non seulement dans la zone d'apex courbe, mais aussi au niveau des éléments linéaires des poutres (cf. Figure 7.16). Cependant, compte tenu de la faible amplitude des contraintes de traction dans ces éléments linéaires, le renforcement sera généralement appliqué uniquement à la zone de la poutre présentant une courbure.
Certaines poutres courbes peuvent être exemptes d'éléments linéaires. Dans ce cas, si nécessaire, le renforcement devra être appliqué à la partie de la poutre où la contrainte de traction perpendiculaire au fil dépassera 80 % de la contrainte de traction maximale perpendiculaire au fil, soit généralement à mi-travée.
En ce qui concerne les poutres à double décroissance, il conviendra, si nécessaire, d'appliquer le renforcement à la zone d'apex de façon symétrique par rapport à la mitravée, sur une zone de la poutre d'une longueur égale à la hauteur de la poutre à l'apex.
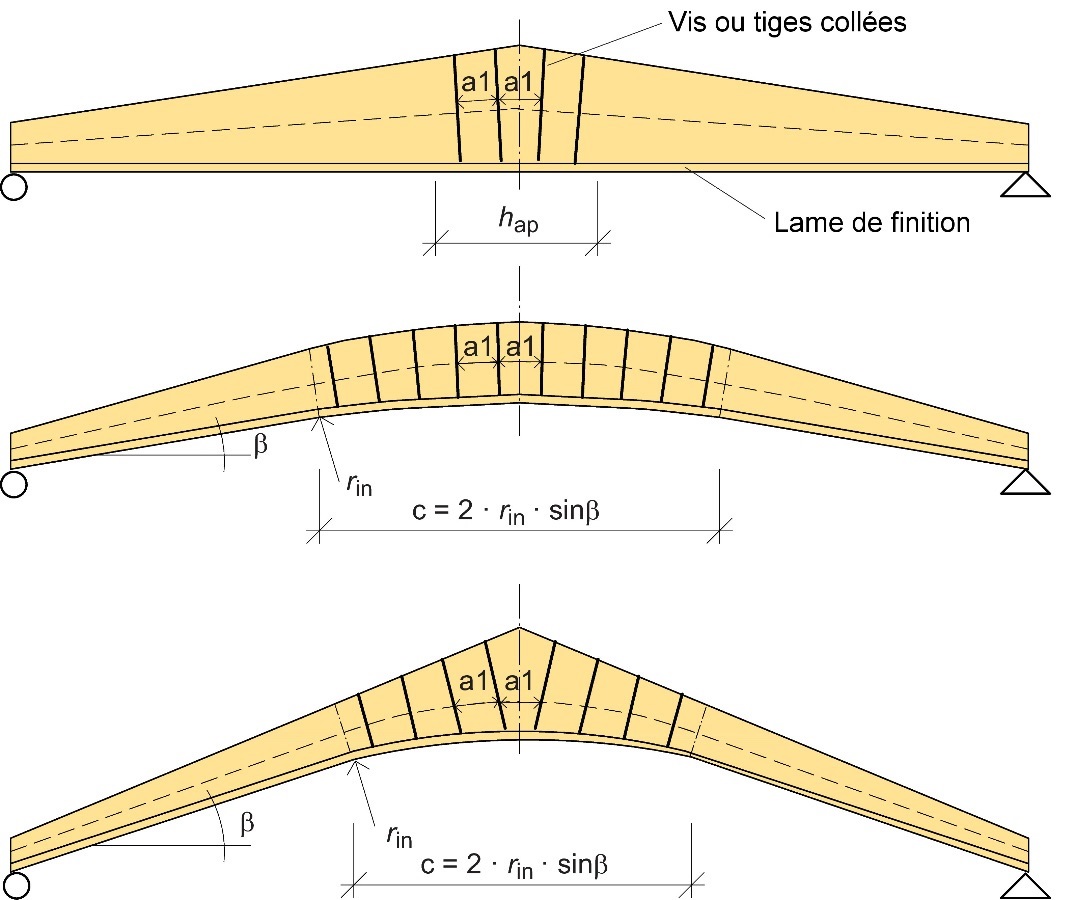
Figure 7.19 : Renforcement de poutres à double décroissance, courbes et bananes.
La proposition de calcul ci-après tient compte de la force résultante de traction de façon simplifiée : on suppose que dans la moitié centrale de la zone d'apex, la contrainte de traction maximale est présente, tandis que dans les zones (« quarts ») extérieures, on présume la présence d’une contrainte égale aux deux tiers de la valeur maximale.
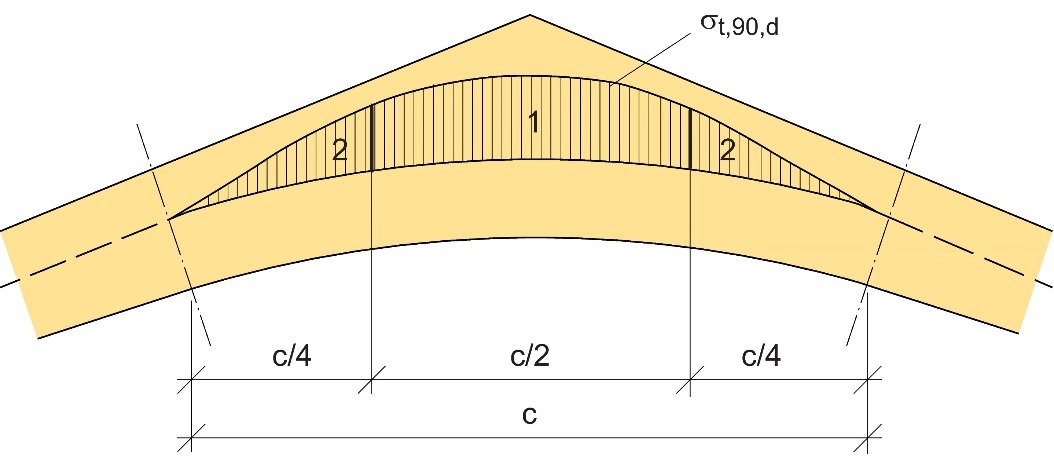
Figure 7.20 : Définition de la « moitié centrale (1) » et des « quarts extérieurs (2) » de l'apex dans une poutre banane.
La force de traction de calcul intervenant dans l’élément de renforcement (à savoir à chaque tige) de la moitié centrale de l'apex est alors exprimée comme suit :

Où :
σt,90,d correspond à la contrainte de traction de calcul perpendiculaire au fil déterminée selon l'Éq. 7.13.
b correspond à la largeur de la poutre.
a1 correspond à l'espacement de l’élément de renforcement le long de la poutre (recommandation : 250 mm≤ a1 ≤ 0,75·hap, où hap correspond à la hauteur de poutre à l'apex).
n correspond au nombre de groupes de barres d’armature perpendiculaires à l'axe longitudinal de la poutre (n=1 ou 2 ; cf. Figure 7.21).

Figure 7.21 : Définition de « n » et de a1 dans l'Éq. 7.26 et l'Éq. 7.27 (« n » correspond au nombre de groupes de barres
d’armature perpendiculaires à l'axe longitudinal de la poutre). dr désigne le diamètre extérieur de filetage de l'élément de
renforcement.

où :
Rax,d correspond à la force axiale de calcul d'un goujon métallique vissé ou collé.
En appliquant l'Éq. 7.28, on retiendra le fait que la force de traction Ft,90,d subit l'opposition des contraintes de cisaillement en surface entre le goujon métallique et le bois, lesquelles ne sont pas réparties de façon uniforme sur la longueur. Cependant, en principe, on suppose que ces contraintes sont uniformément réparties (cf. Figure7.22). Par ailleurs, la partie supérieure du goujon (ou de la vis) est soumise à une traction vers le haut tandis que sa partie inférieure est soumise à une traction vers le bas. C'est pourquoi, dans le cadre de l'Éq. 7.28, la résistance du goujon (ou de la vis) à l'arrachement doit être déterminée pour une longueur égale à lad (cf. Figure 7.22). Dans le cas de vis entièrement filetées ou de goujons entièrement collés sur toute la hauteur de la poutre, il est possible de prendre la moitié de la longueur du goujon (ou de la vis) comme valeur de lad.
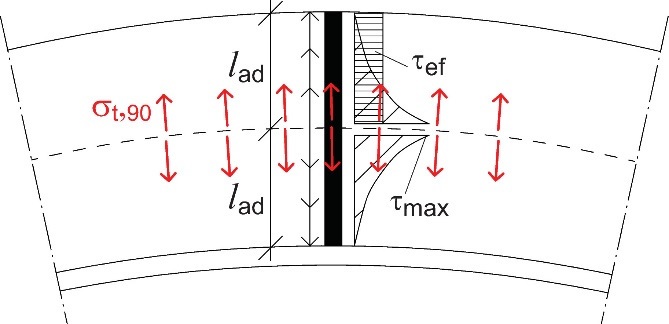
Figure 7.22 : Contrainte de cisaillement dans l'élément de renforcement d'une poutre courbe.

